Exploring polar graphs can be both fascinating and challenging for math enthusiasts. One key concept to understand is the 4costheta equation and its impact on polar graphs.
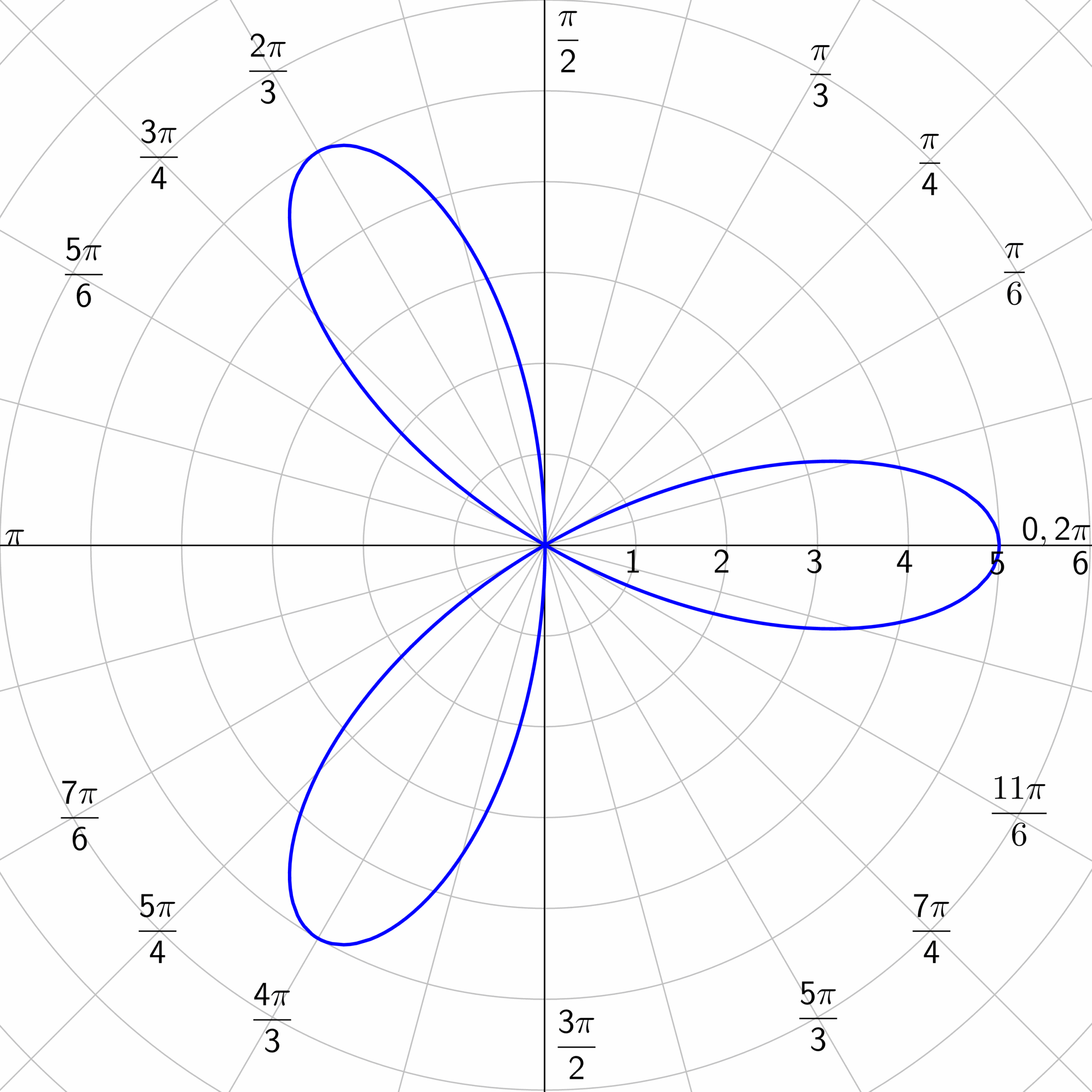
When plotted on a polar coordinate system, 4costheta generates a unique pattern that is influenced by the cosine function. This equation allows us to visualize how the cosine of an angle affects the radius of a point on the graph.
4costheta On Polar Graph
4costheta On Polar Graph
As we trace the curve of 4costheta on a polar graph, we observe a distinct shape that repeats itself every 2pi radians. The graph showcases the relationship between the angle theta and the resulting radius, creating a visually striking pattern.
The 4costheta equation also demonstrates symmetry across the x-axis, with the graph mirroring itself in a graceful and harmonious manner. This symmetry adds to the beauty and complexity of polar graphs, offering a deeper insight into mathematical relationships.
By manipulating the coefficients and functions in the 4costheta equation, mathematicians can create various modifications and explore different graphical outcomes. This experimentation allows for a deeper understanding of how mathematical functions interact and influence each other on a polar graph.
In conclusion, delving into the world of polar graphs and equations like 4costheta can be a rewarding journey for those passionate about mathematics. The intricate patterns and relationships that emerge from these graphs offer a glimpse into the elegance and complexity of mathematical concepts.
How To Express Polar Points Multiple Ways By Changing The Values Of R And Theta Krista King Math Online Math Help
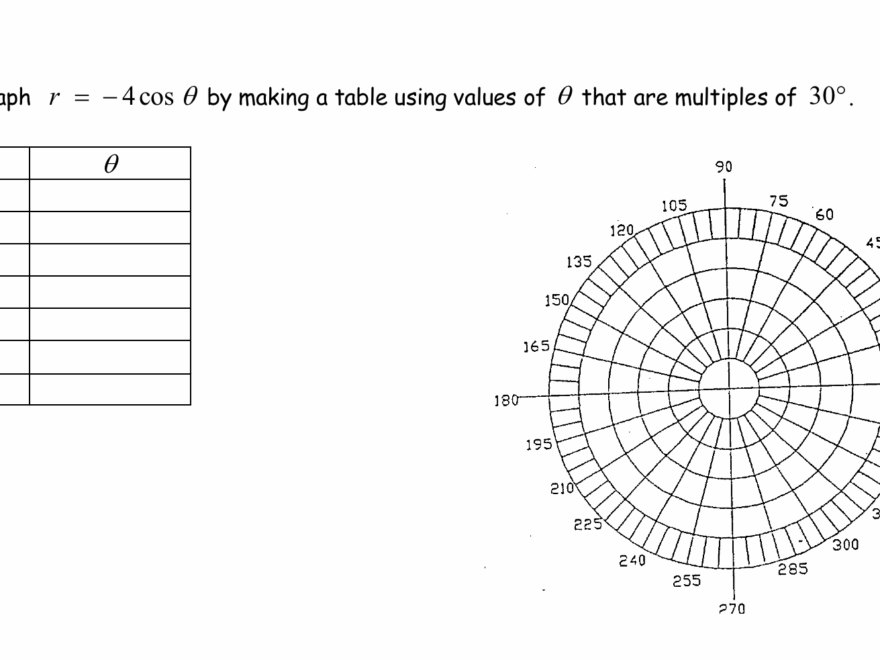
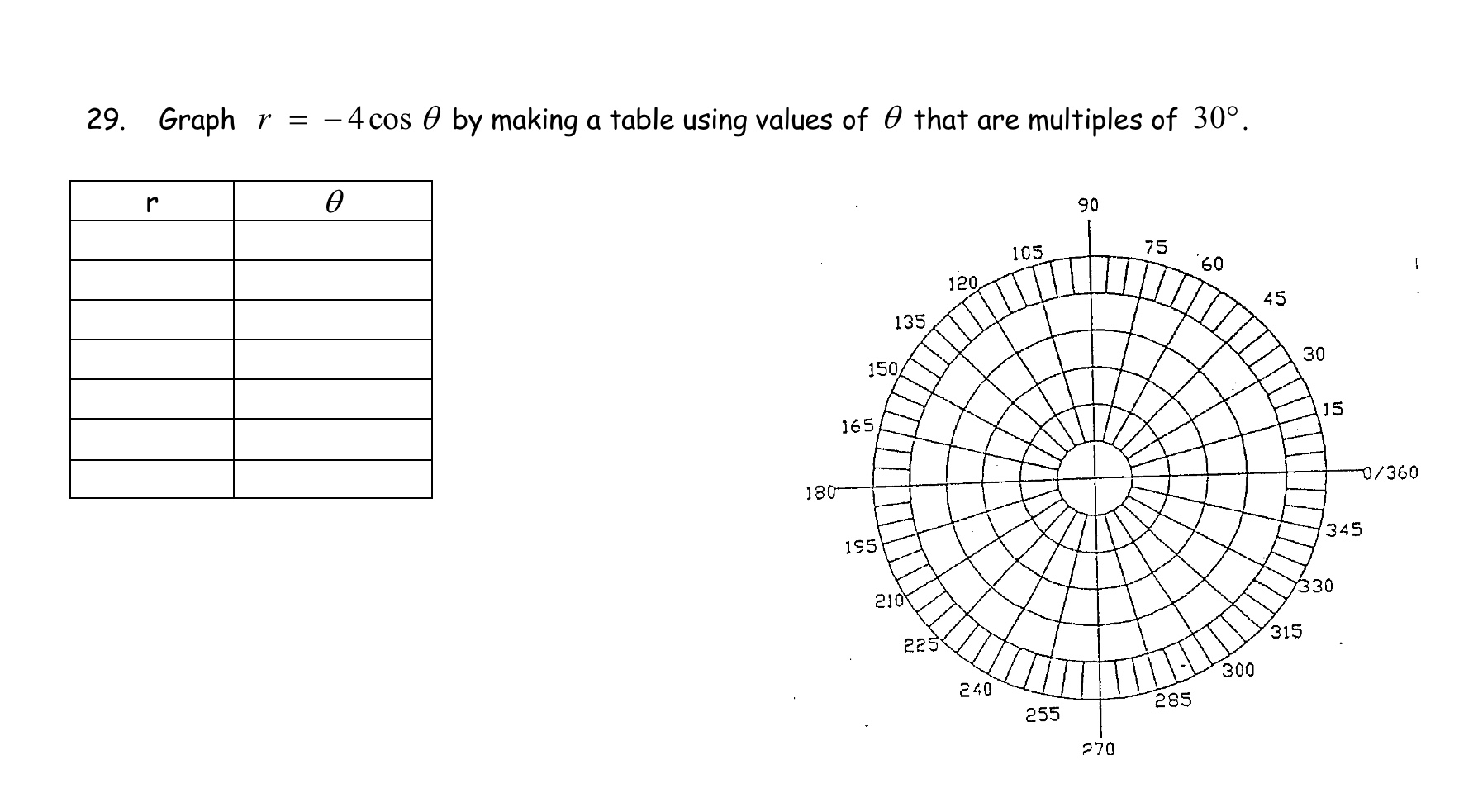
Solved Graph R 4cos Theta By Making A Table Using Values Of Chegg