Are you interested in learning about how to convert Cartesian coordinates to polar coordinates in graphing? It’s a useful skill to have, especially if you’re studying math or physics. By understanding this conversion process, you can easily plot points in a polar coordinate system.
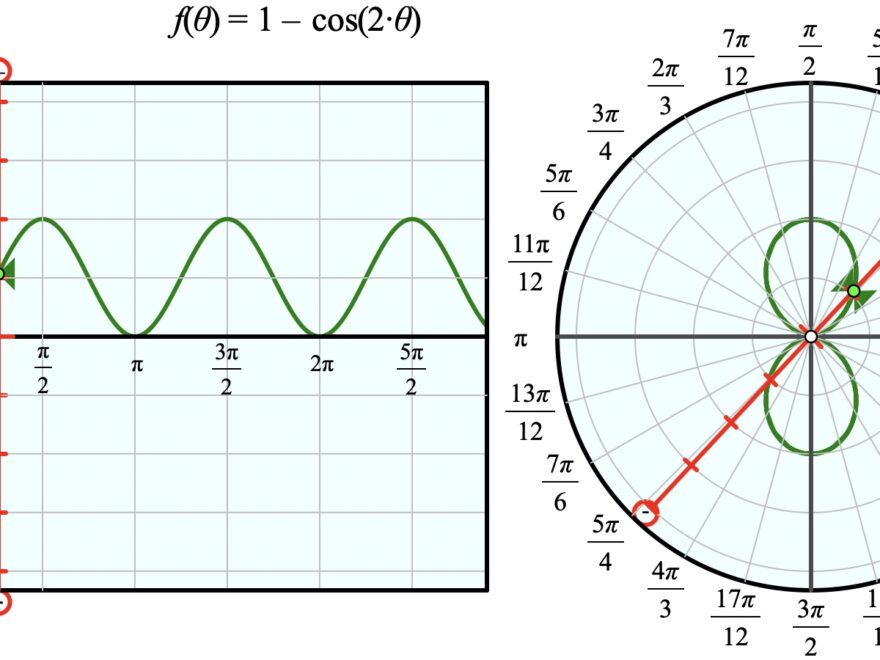
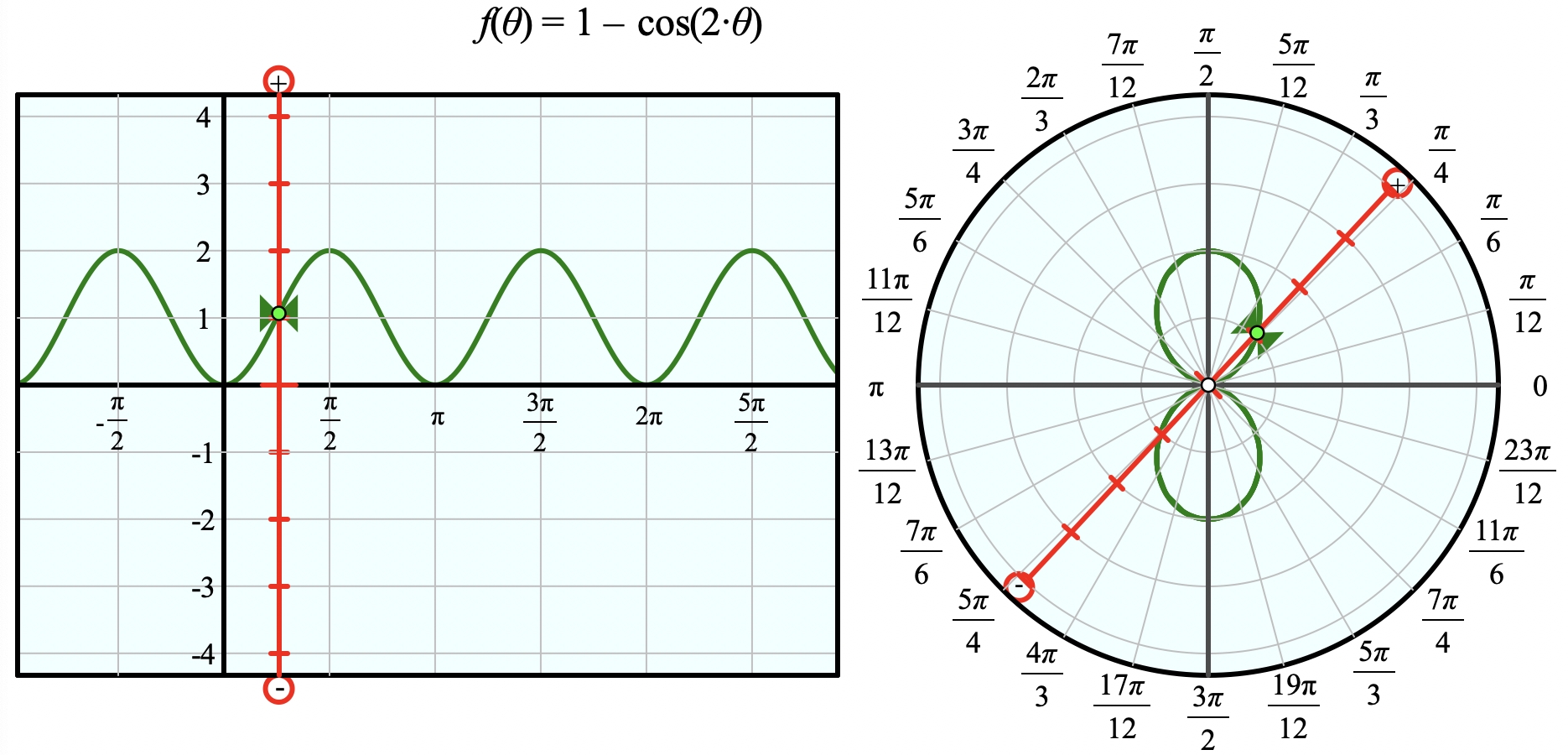
When you convert Cartesian coordinates to polar coordinates, you’re essentially changing the way you describe a point on a graph. Instead of using x and y coordinates, you’ll use r (radius) and θ (angle). This can be particularly helpful when working with circular or radial patterns.
Cartesian To Polar Graphing
Cartesian To Polar Graphing
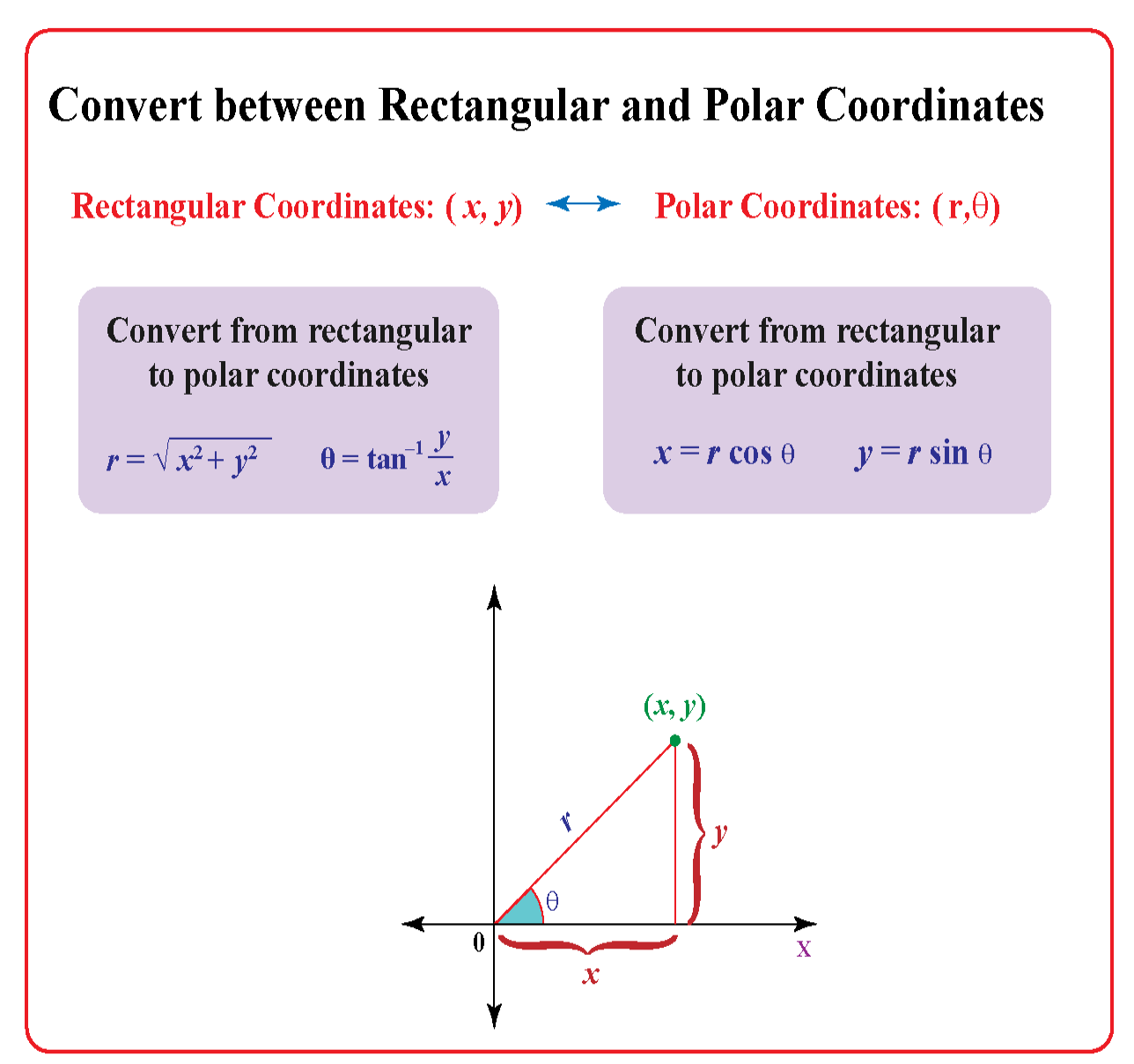
To convert from Cartesian to polar coordinates, you can use the following formulas: r = √(x^2 + y^2) for the radius and θ = tan^(-1)(y/x) for the angle. These equations allow you to easily transform a point from one system to the other.
One common mistake when converting coordinates is mixing up the signs of x and y. Remember that in the Cartesian system, x is positive to the right and y is positive upwards. However, in the polar system, r is always positive, and θ is measured counterclockwise from the positive x-axis.
By mastering the conversion process from Cartesian to polar coordinates, you’ll be able to plot points, draw curves, and solve problems more efficiently in a polar coordinate system. This skill can be particularly useful in fields such as engineering, physics, and astronomy.
So, the next time you need to graph a point in a polar coordinate system, remember the simple formulas for converting from Cartesian coordinates. With a little practice, you’ll become a pro at Cartesian to polar graphing in no time!
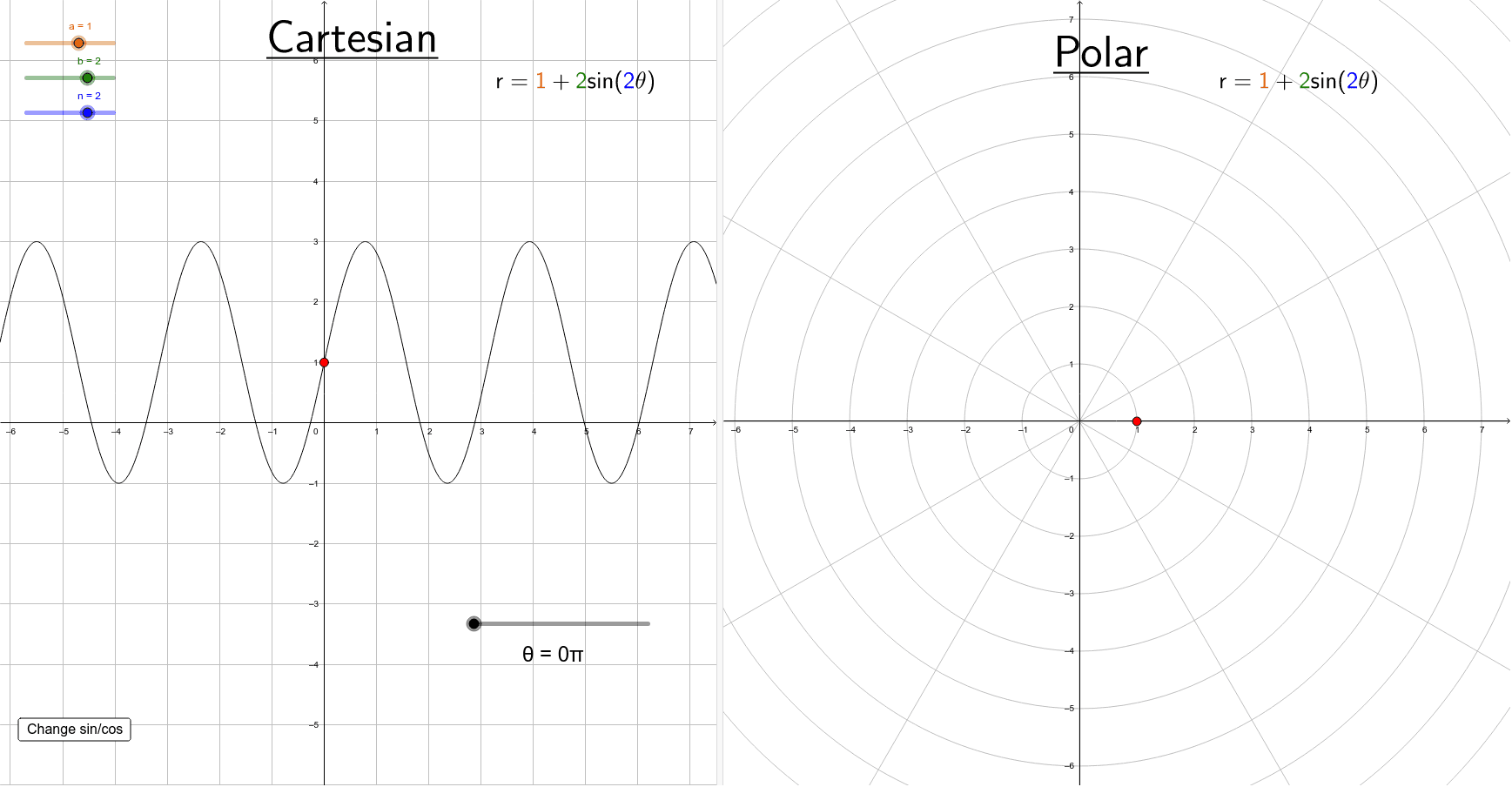
Converting Cartesian Graphs Into Polar Graphs GeoGebra
Cartesian And Polar Graphs Sine Of The Times