Are you familiar with the concept of a circle on a graph? It’s a fundamental geometric shape that plays a crucial role in mathematics and various fields of science.
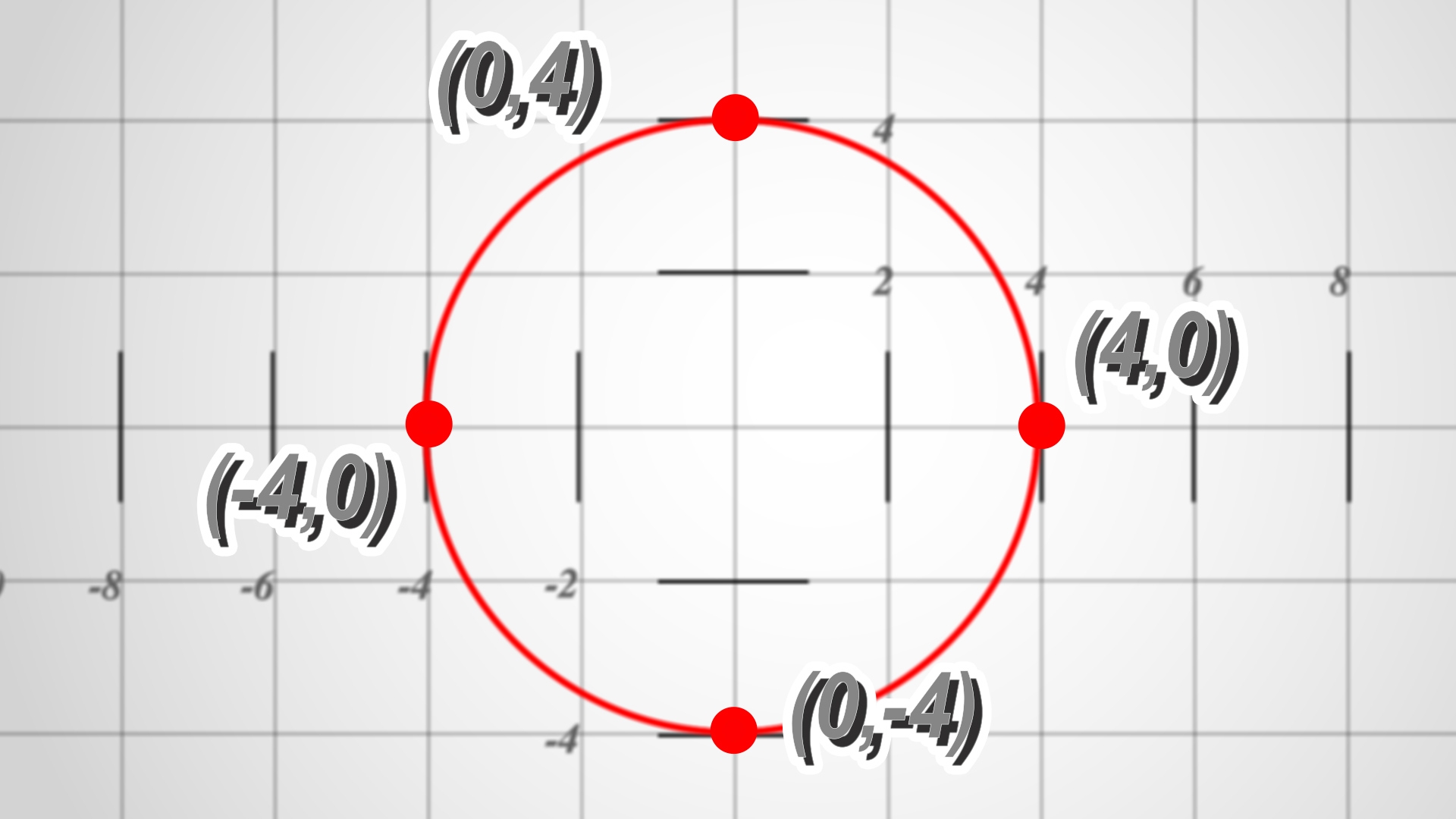
When you plot a circle on a graph, you create a closed curve where all points are equidistant from the center. This simple yet elegant shape has numerous applications in real-world scenarios.
Circle On A Graph
Exploring the Beauty of a Circle On A Graph
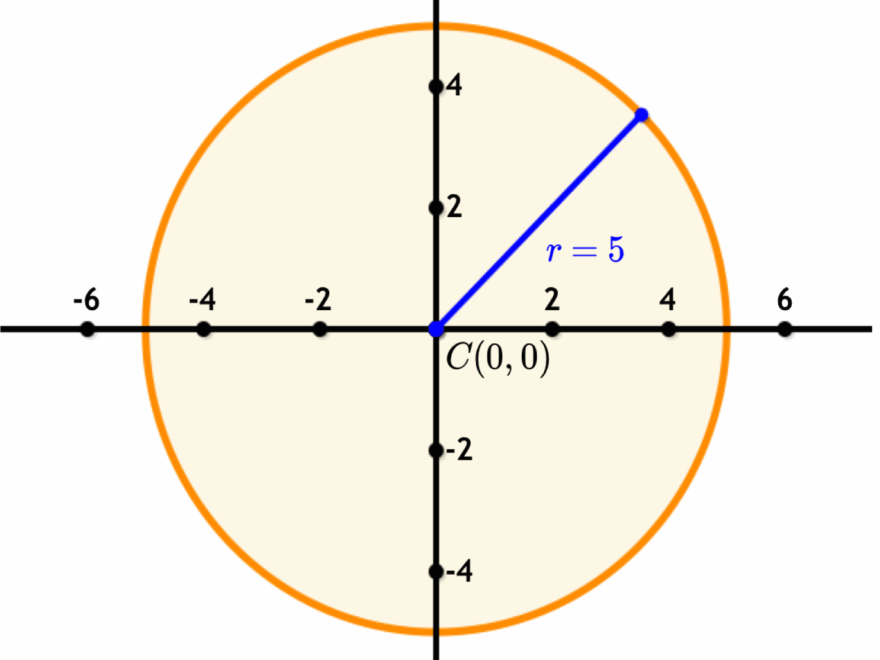
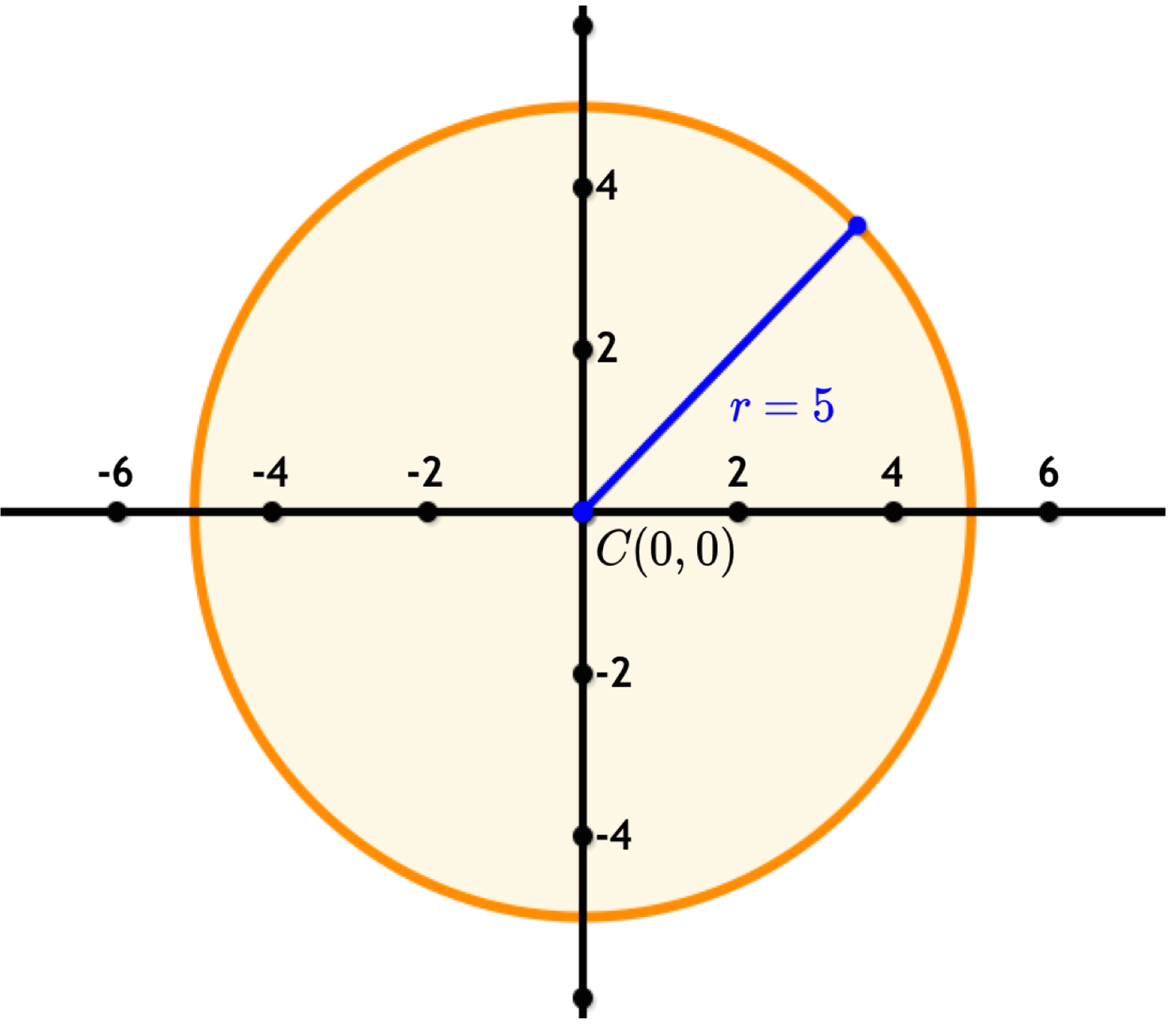
One of the key properties of a circle on a graph is its circumference, which is the total distance around the outer edge. This value can be calculated using the formula C = 2πr, where r is the radius of the circle.
In addition to the circumference, circles also have a unique area that can be determined using the formula A = πr^2. This formula allows us to calculate the amount of space enclosed by the circle on a graph.
Furthermore, circles play a crucial role in trigonometry, where they are used to define sine, cosine, and tangent functions. These functions help us understand the relationships between angles and sides of a right triangle.
Whether you’re studying geometry, physics, or engineering, a solid understanding of circles on a graph is essential. By mastering the properties and formulas associated with circles, you can solve complex problems with ease.
In conclusion, a circle on a graph may seem like a simple shape, but its significance cannot be understated. From calculating areas to defining trigonometric functions, circles play a vital role in mathematics and beyond.
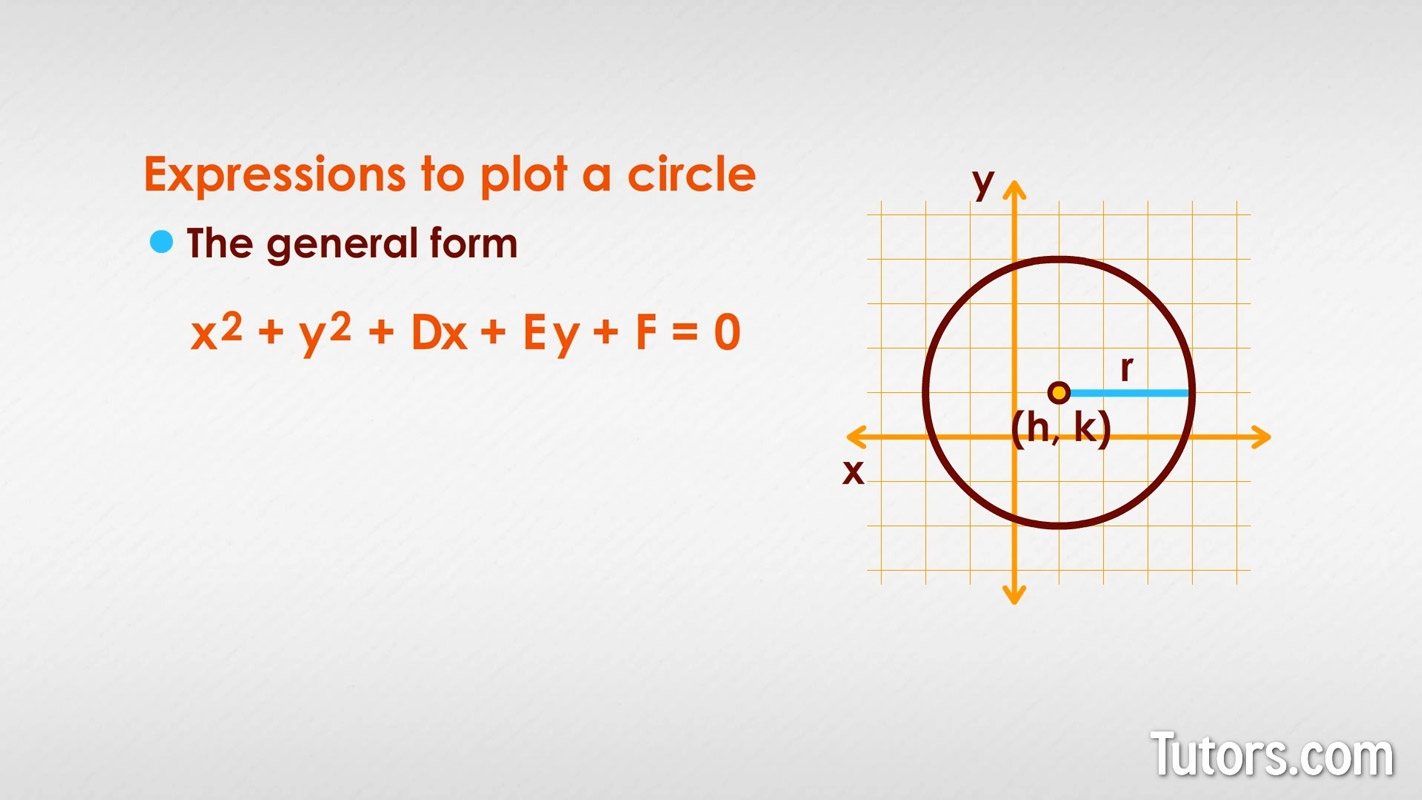
How To Graph A Circle 4 Easy Steps Equations Examples Video
Circles Mixed And Semi Circles Class XI Maths India Class XI Mathspace