Exploring the world of mathematics can be both fascinating and challenging. One concept that often intrigues students is the use of Curvillinear Polar Coordinates on a graph. These coordinates provide a unique way to represent points in a plane.
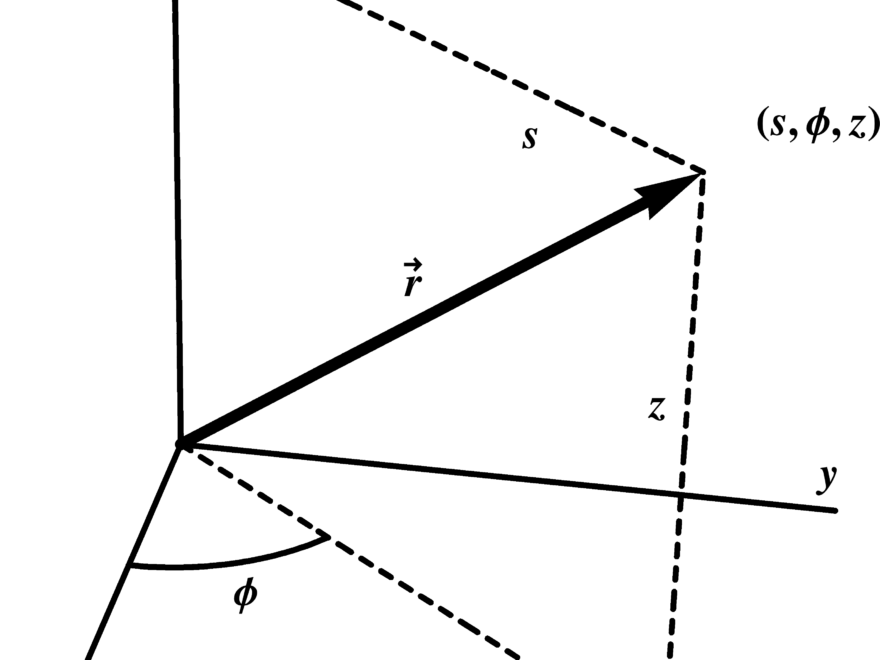
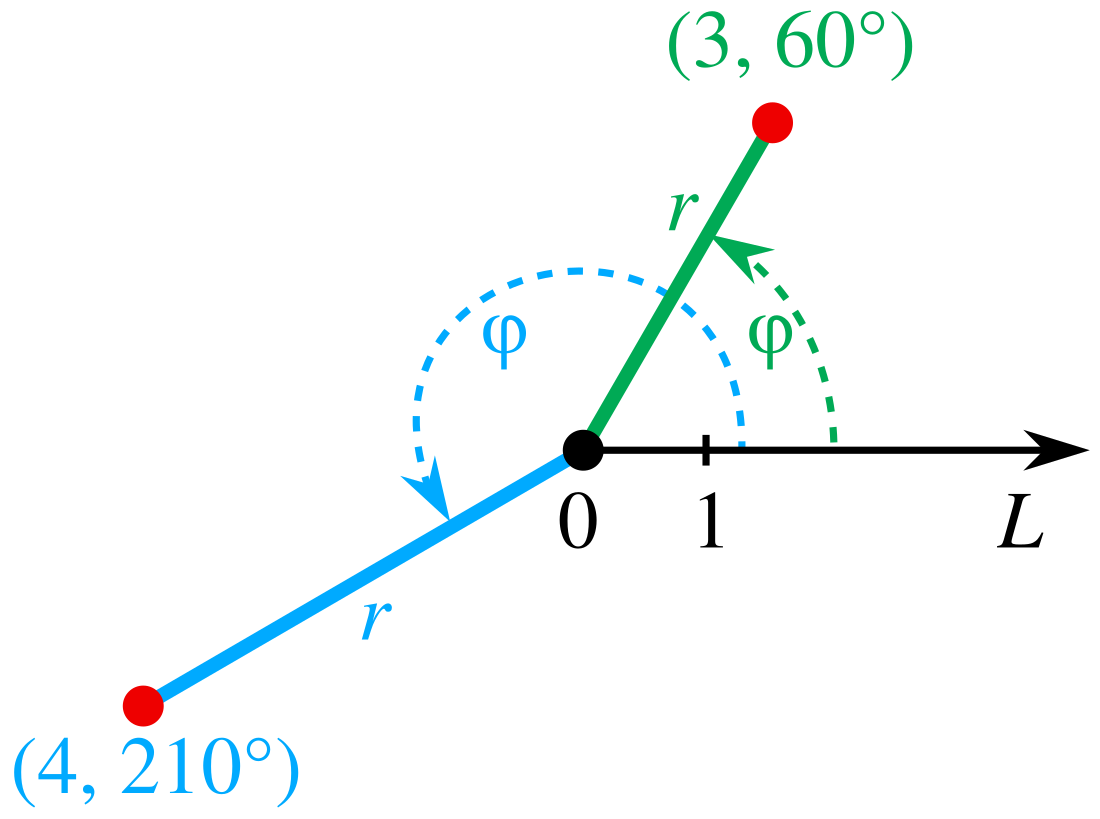
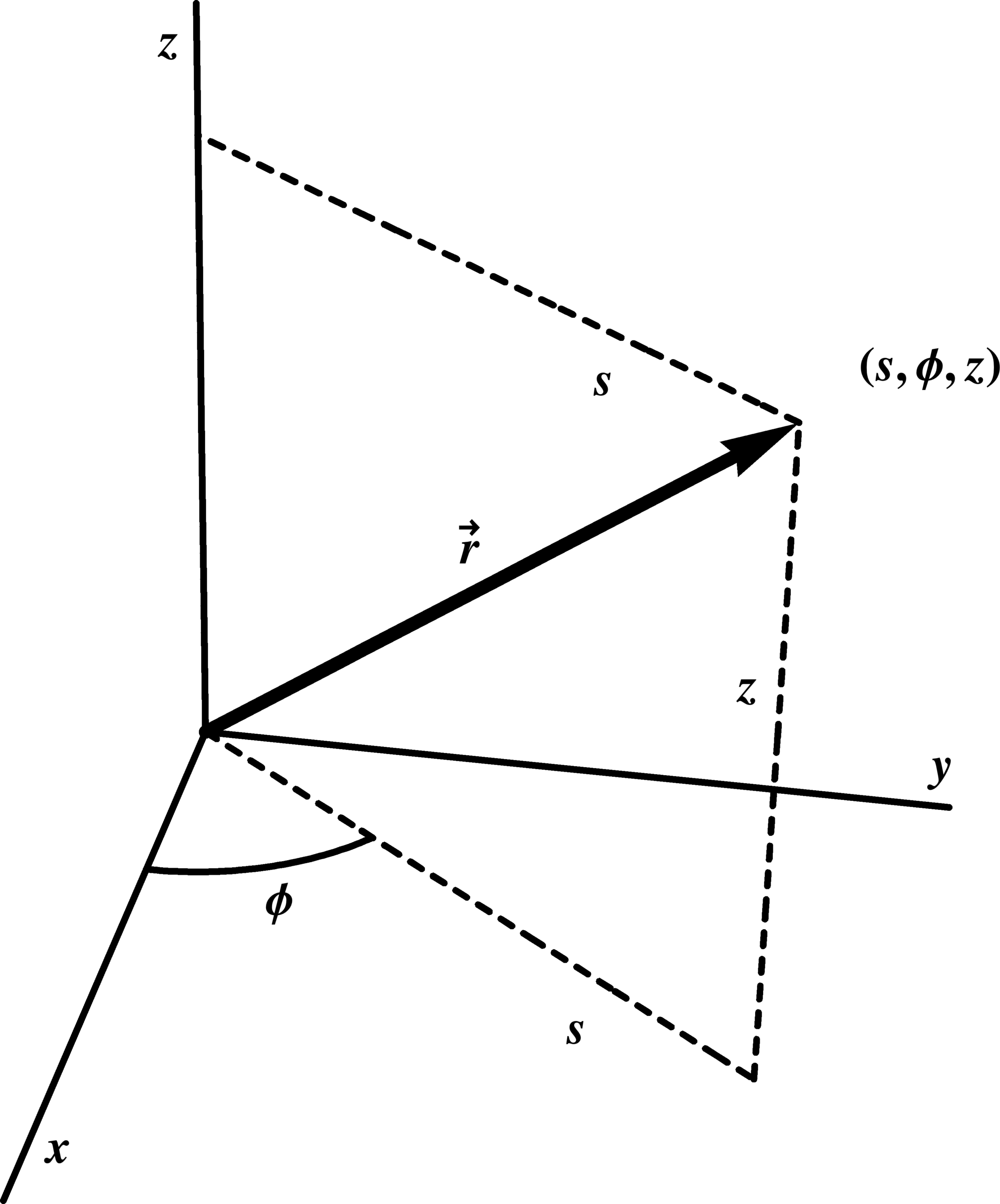
When working with Cartesian coordinates, we use x and y axes to locate points. However, in polar coordinates, we use an angle and a distance from the origin. Curvillinear polar coordinates take this concept one step further by allowing for curved axes on the graph.
Curvill8inear Polar Coordniates On A Graph
Curvillinear Polar Coordinates On A Graph
Imagine a graph where the axes are not straight lines but instead follow a curve. This is where curvillinear polar coordinates come into play. By using these coordinates, we can represent points in a way that is more suited to certain types of problems.
One common example of curvillinear polar coordinates is the use of polar coordinates on a sphere. Instead of using traditional Cartesian coordinates, which may not be ideal for representing points on a curved surface, we can use polar coordinates that align with the shape of the sphere.
Another application of curvillinear polar coordinates is in the study of complex functions. By using a curvillinear grid on the complex plane, mathematicians can gain insights into the behavior of functions that may not be apparent when using traditional Cartesian coordinates.
In conclusion, Curvillinear Polar Coordinates on a graph offer a unique perspective on representing points in a plane. By embracing these coordinates, mathematicians can explore new ways of visualizing and solving problems that may be challenging with traditional Cartesian coordinates.
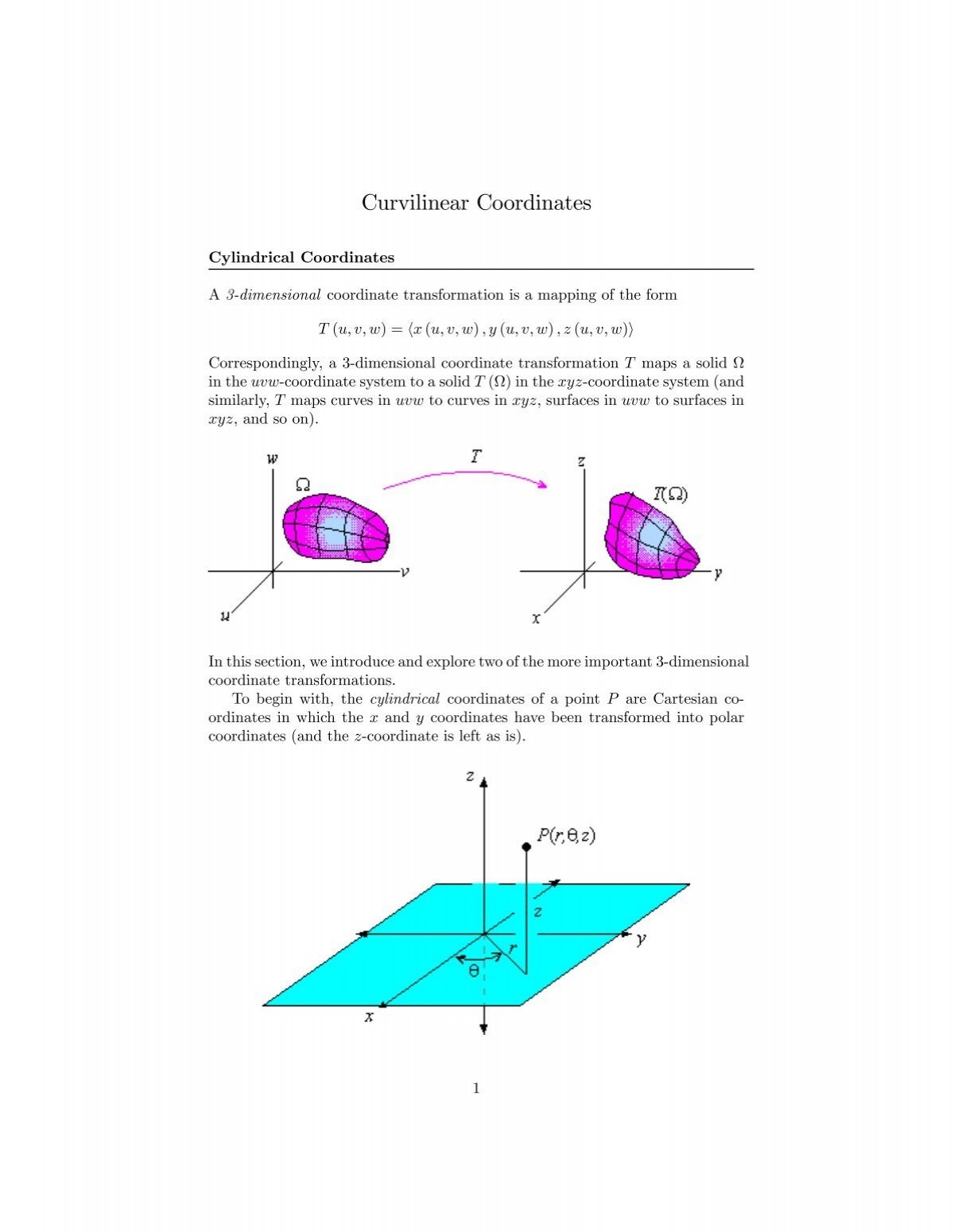
Curvilinear Coordinates
Curvilinear Coordinates