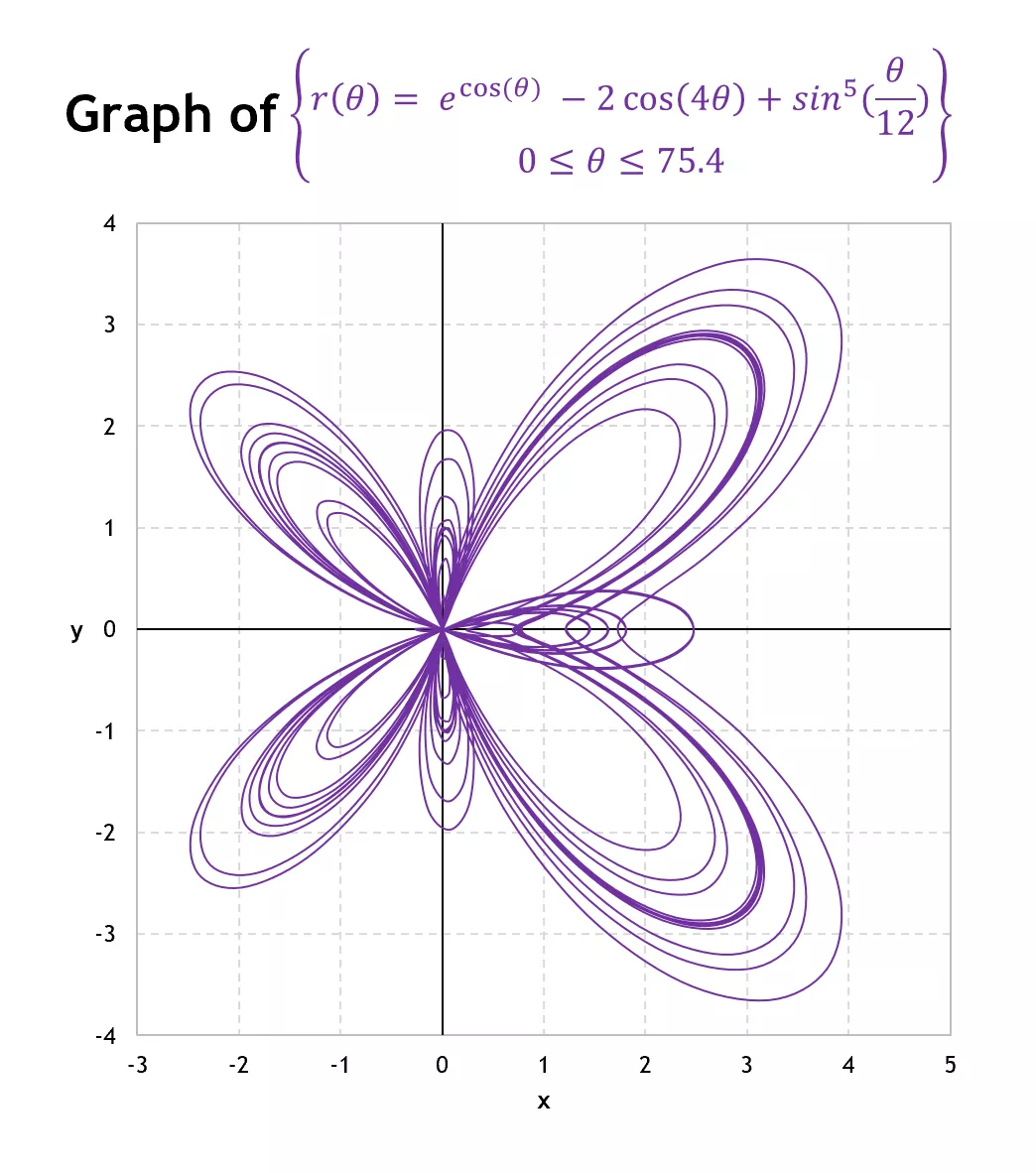
Have you ever heard of the polar coordinate graph? It’s a unique way to represent points in the plane using angles and distances from the origin. This type of graph can be incredibly useful in various fields, from mathematics to physics.
When working with polar coordinates, instead of using the traditional x and y axes, you’ll use an angle (usually denoted by θ) and a distance from the origin (denoted by r). This allows you to describe the location of a point in a more intuitive way, especially when dealing with circular or radial patterns.
O Polar Coordinate Graph
The Beauty of the Polar Coordinate Graph
One of the key advantages of the polar coordinate graph is its ability to simplify complex problems. For example, when graphing functions with radial symmetry, such as circles or spirals, polar coordinates can make the process much more straightforward.
In addition to simplifying graphing tasks, polar coordinates can also be used to represent physical phenomena more accurately. For instance, in physics, polar coordinates are often used to describe the motion of objects in circular or rotational paths.
Another benefit of the polar coordinate system is its versatility. While it may seem unfamiliar at first, once you get the hang of it, you’ll find that polar coordinates can be a powerful tool for visualizing and analyzing a wide range of mathematical and physical concepts.
So, next time you come across a problem that involves circular or radial symmetry, consider using the polar coordinate graph. You might be surprised at how much easier it can make your life!
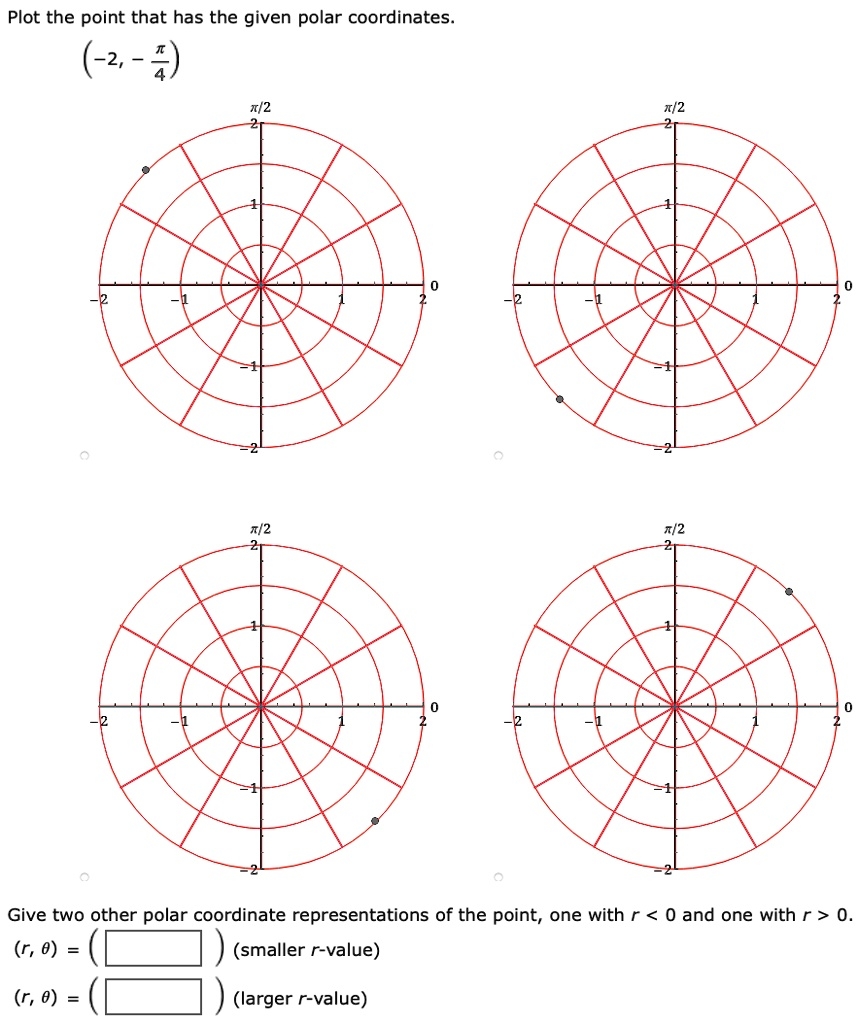
Plot The Point That Has The Given Polar Coordinates 2 4 Give Two Other Polar Coordinate
Ios Polar Coordinate Point Generation Function Upper Bound Is Not 2Pi For Theta Stack Overflow