Are you struggling with understanding polar coordinate graphs in Further Mathematics? Don’t worry, you’re not alone! These graphs can be tricky to grasp at first, but with a little practice, you’ll soon be a pro.
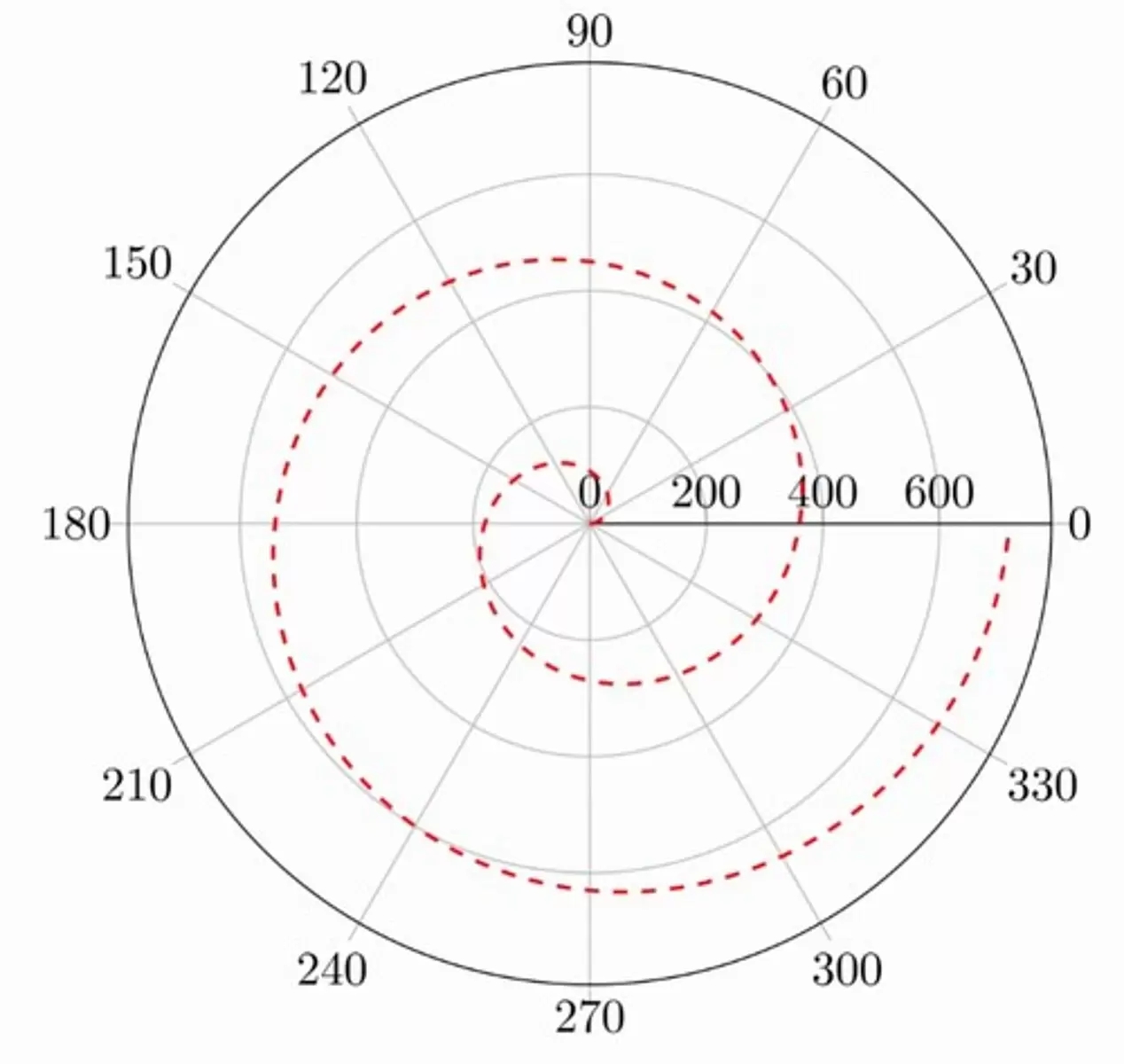
In polar coordinates, points are represented by their distance from the origin (r) and the angle they make with the positive x-axis (θ). This system is useful for representing circular and other periodic functions.
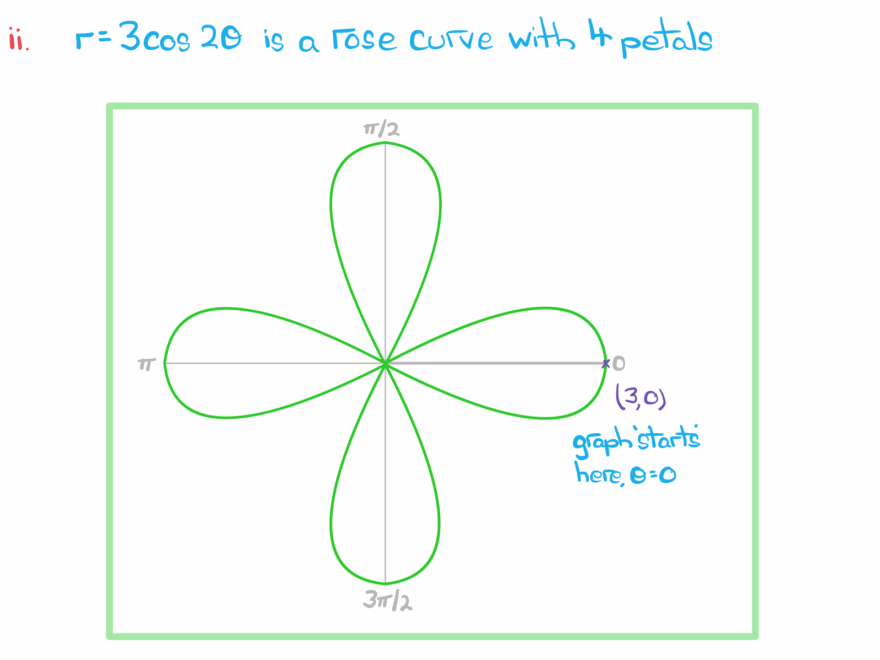
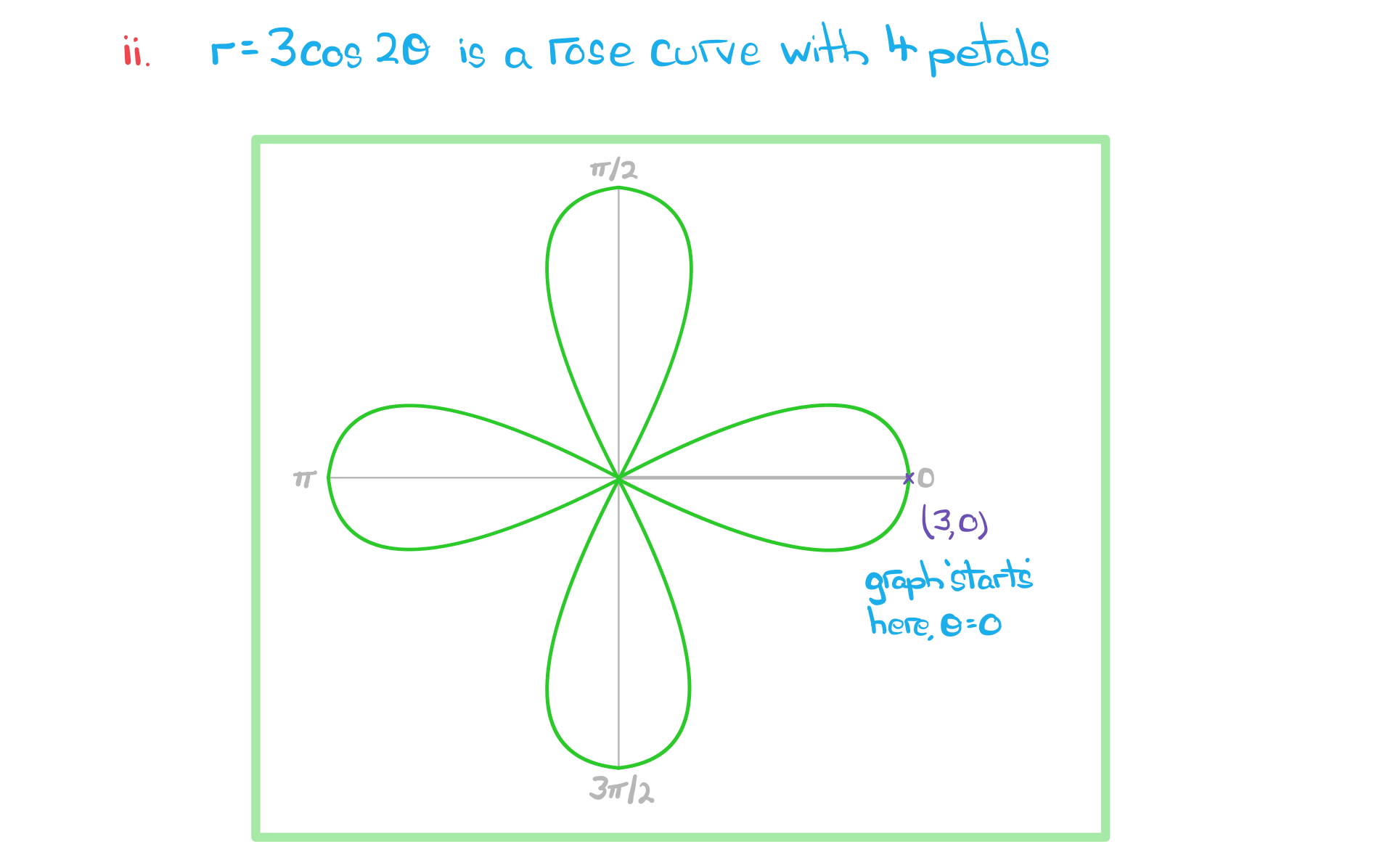
Further Mathematics Polar Coordinate Graph
Further Mathematics Polar Coordinate Graph
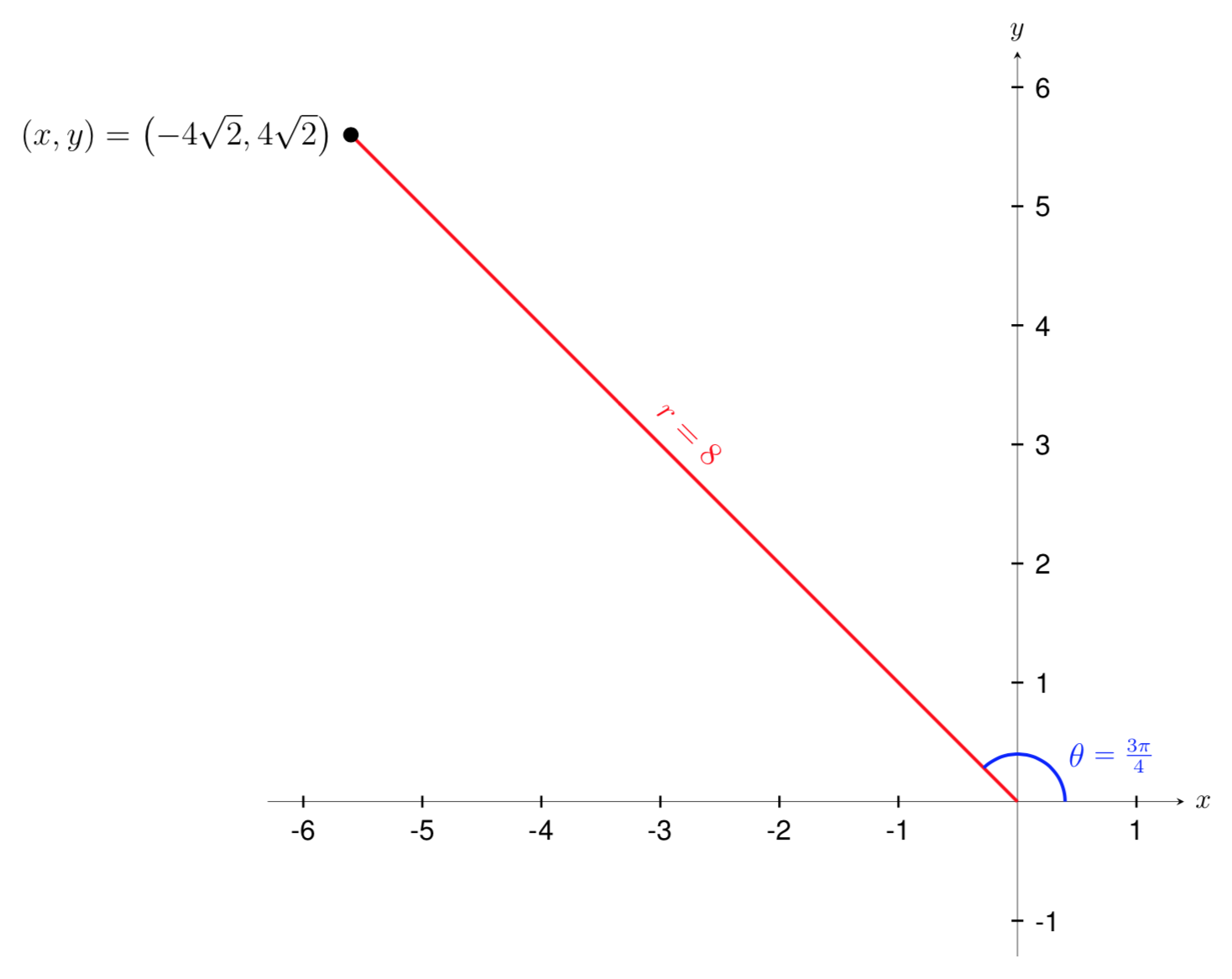
To plot a point in polar coordinates, start by drawing a ray from the origin at the specified angle θ. Then, measure the distance r along this ray to locate the point. Repeat this process for all points to create the graph.
One common polar graph is the circle, where all points are equidistant from the origin. The equation for a circle in polar coordinates is r = a, where ‘a’ represents the radius of the circle.
Another important polar graph is the cardioid, which resembles a heart shape. It is represented by the equation r = a(1 + cos θ) or r = a(1 – cos θ), depending on the orientation of the graph.
By understanding the basic shapes and equations of polar graphs, you’ll be able to tackle more complex functions and curves in Further Mathematics. Practice plotting points and sketching graphs to improve your skills.
Don’t get discouraged if polar coordinate graphs seem challenging at first. With patience and practice, you’ll soon become comfortable with this unique way of representing functions and curves. Keep practicing, and you’ll master Further Mathematics in no time!
R Theta 2 Axis Stages Precision Motion Control PI
Polar Coordinates Edexcel A Level Further Maths Revision Notes 2017