Are you struggling to understand the basics of log function graphs? Don’t worry, you’re not alone! Many people find this topic challenging at first, but with a little guidance, you’ll be graphing like a pro in no time.
In this article, we’ll break down the concept of Basic Log Function Graphs in a simple and easy-to-understand way. By the end, you’ll have a solid grasp of how to plot these graphs and interpret their meaning.
Basic Log Function Graph
Basic Log Function Graph
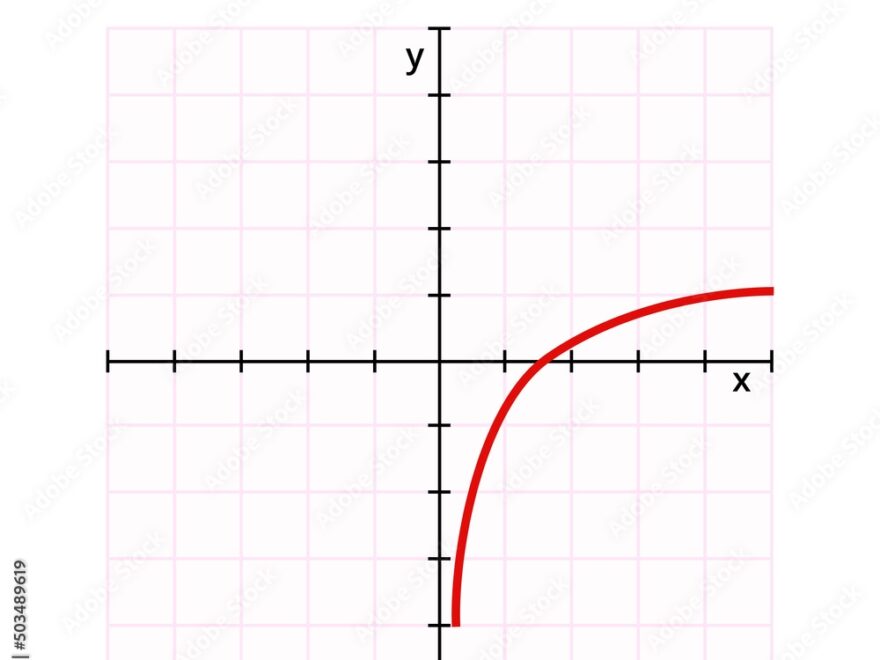
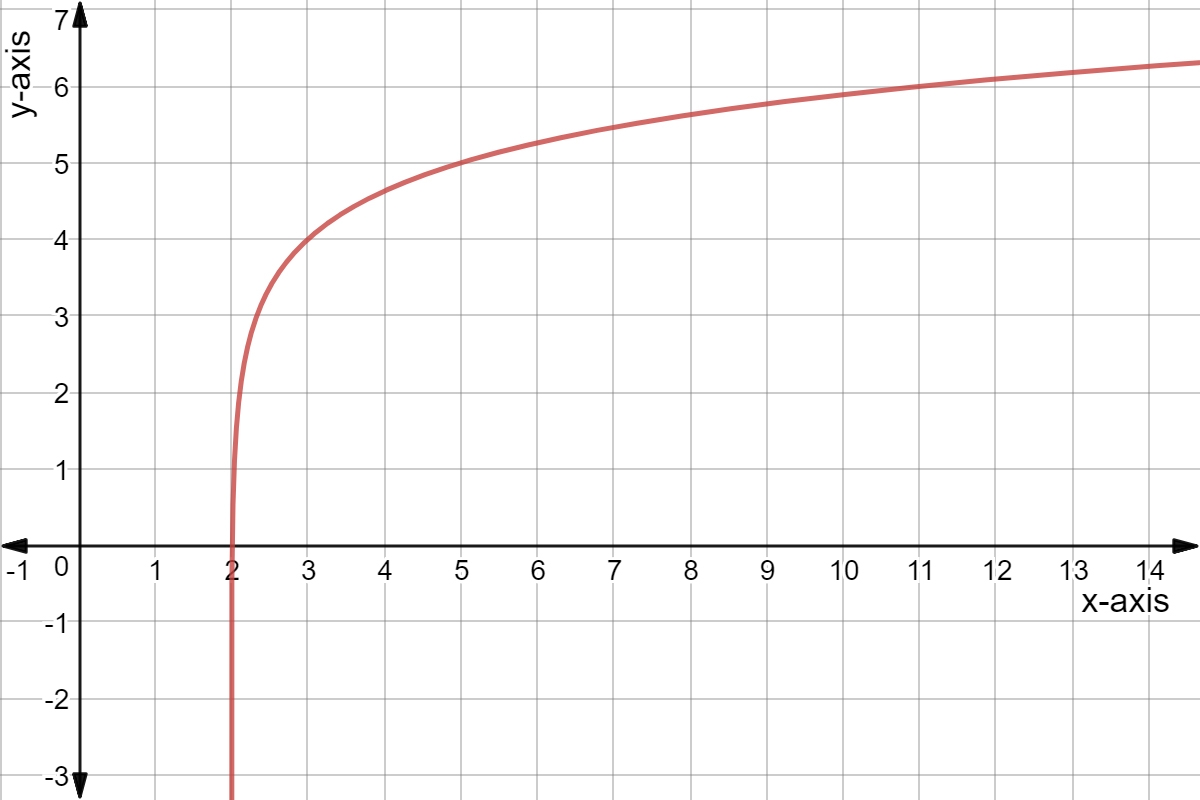
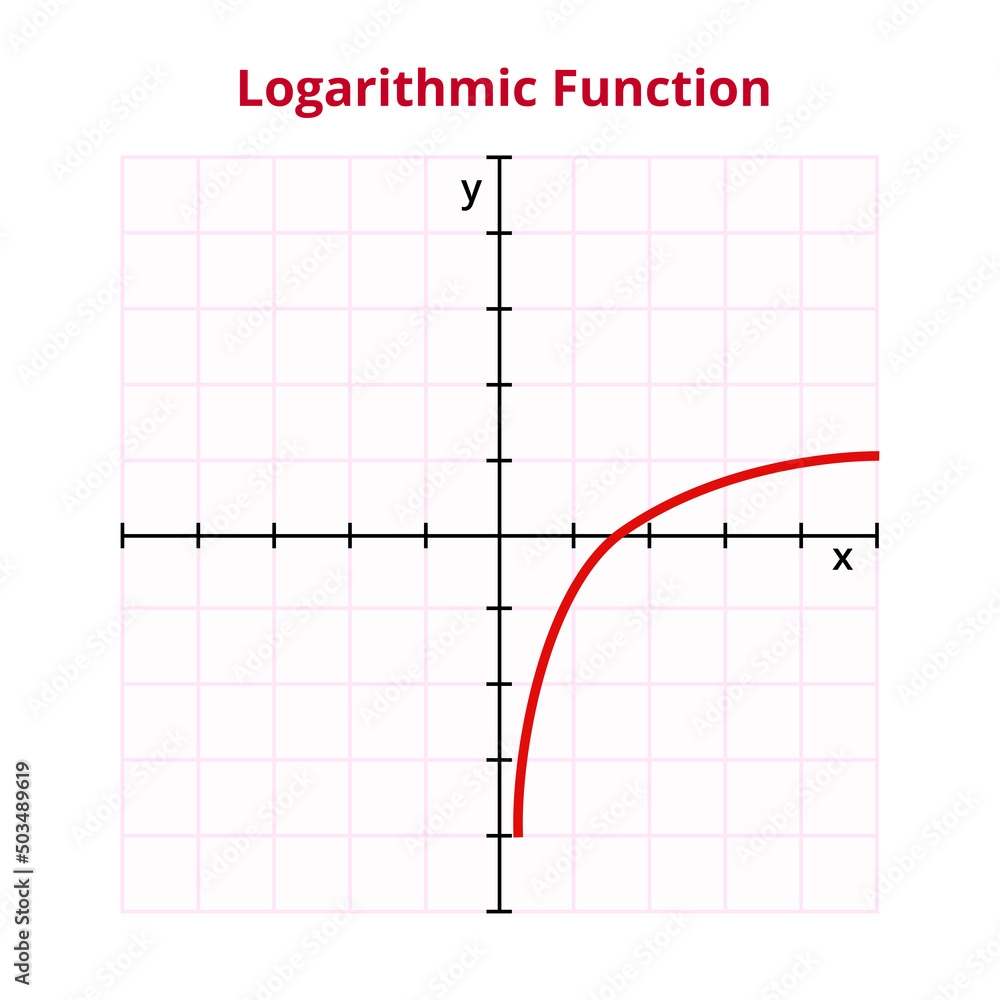
A log function graph is a visual representation of a logarithmic equation. These graphs have a characteristic shape that differs from linear or exponential functions. The graph typically consists of a curve that approaches but never touches the x-axis.
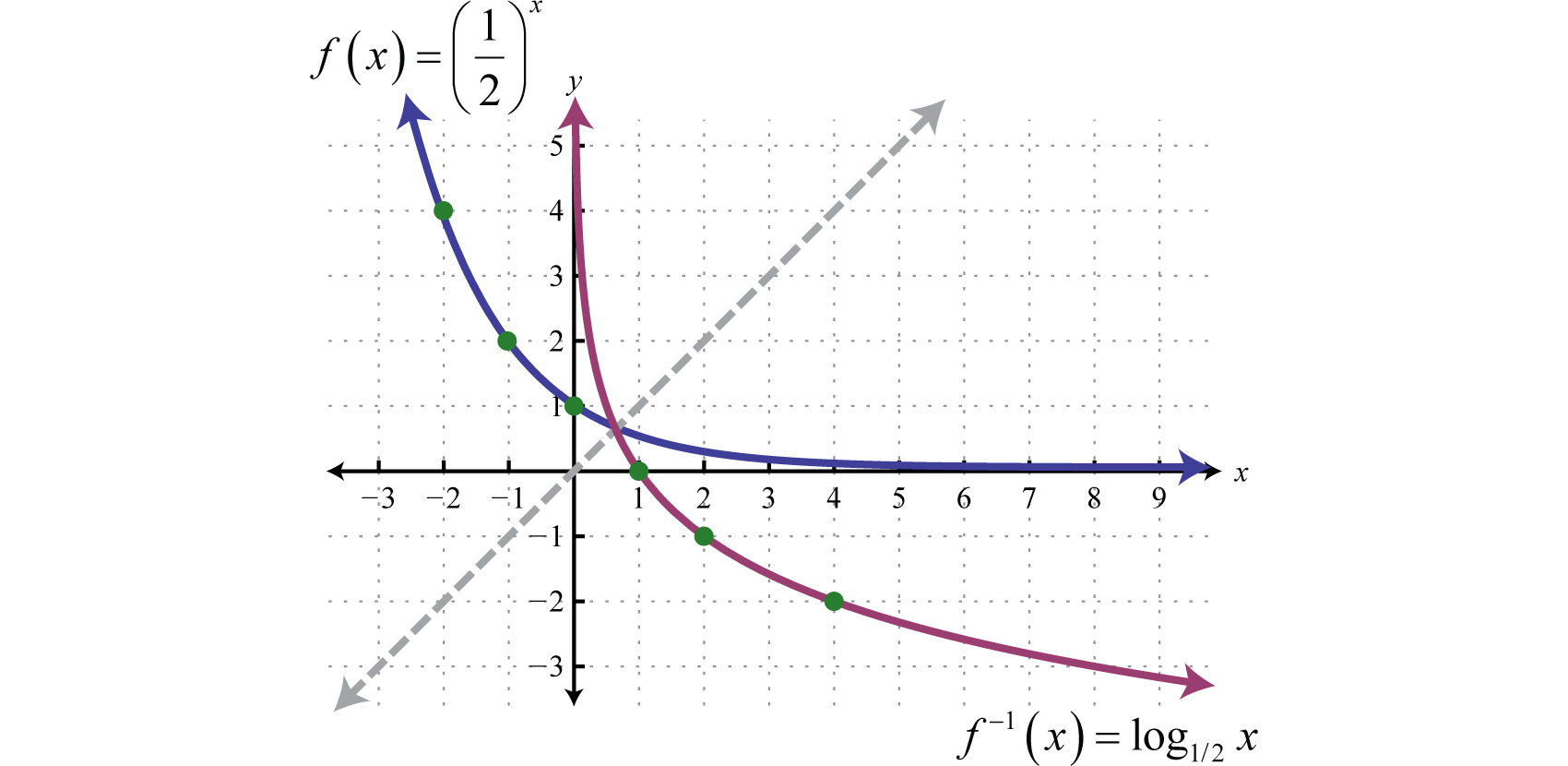
When graphing a basic log function, it’s essential to understand the key components. The logarithmic function is written as y = log_b(x), where b is the base of the logarithm. The base determines the shape and behavior of the graph.
As x approaches positive infinity, the graph of a log function approaches but never reaches the x-axis. On the other hand, as x approaches zero, the graph approaches negative infinity. Understanding these behaviors is crucial for accurately plotting log function graphs.
One common mistake when graphing log functions is forgetting about the domain restrictions. Logarithmic functions are only defined for positive values of x, so be sure to exclude any negative or zero values when plotting the graph.
In conclusion, mastering the basics of log function graphs may take some practice, but with patience and perseverance, you’ll become proficient in no time. Remember to pay attention to the key components, such as the base of the logarithm and domain restrictions, to accurately plot these graphs.
Asymptotes Of Logarithmic Graphs Expii
Vector Graph Or Chart Of Logarithmic Function With Formula Y Log X Fx Ln X Logarithm Inverse Function To Exponentiation Mathematical Operation Basic Function Graph With Grid And Coordinates Stock