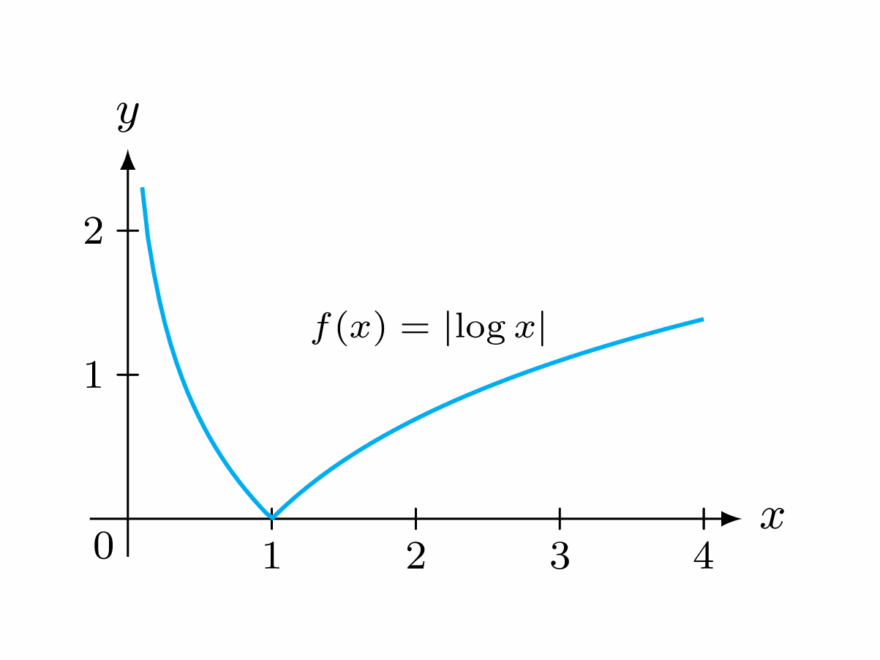Have you ever wondered about the graph of a log function? It’s a fascinating topic that can seem intimidating at first, but once you break it down, it’s actually quite simple to understand.
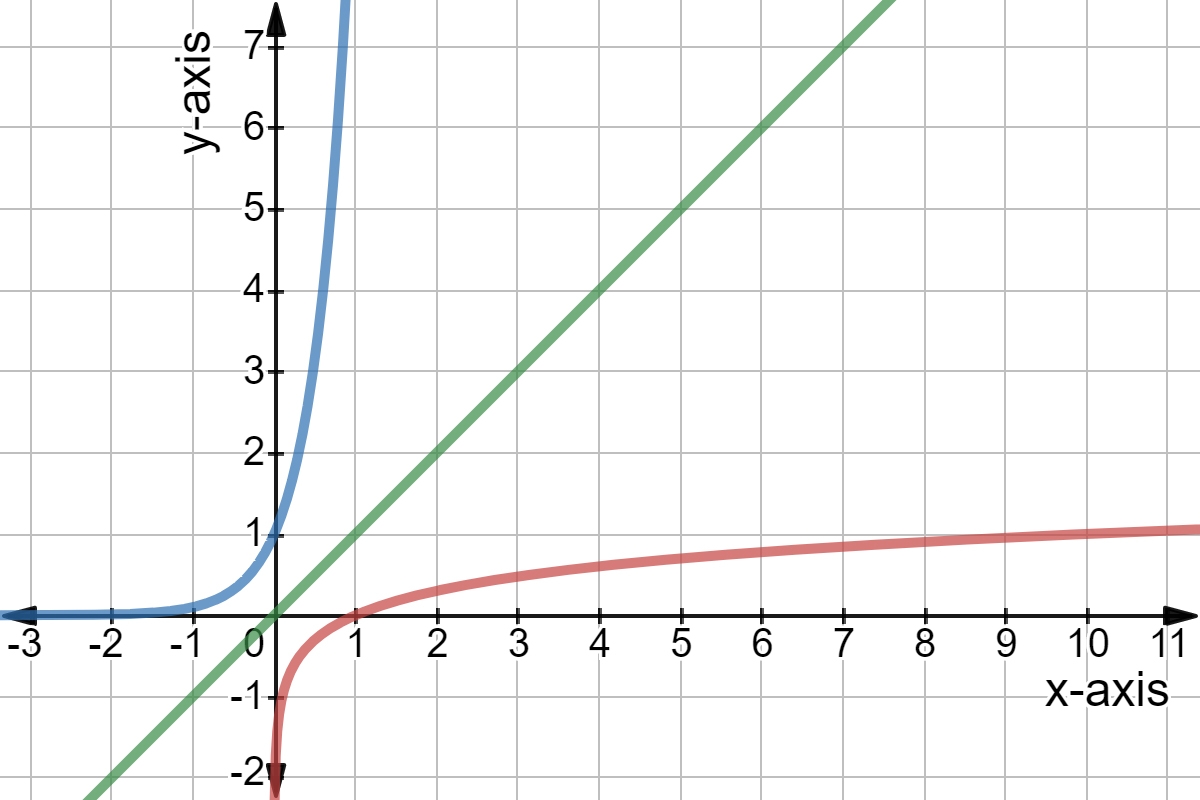
Logs are the inverse of exponential functions, so they essentially “undo” the work of exponentials. The graph of a log function reflects this relationship in a visually striking way.
Graph Of Log Function
Exploring the Graph of Log Function
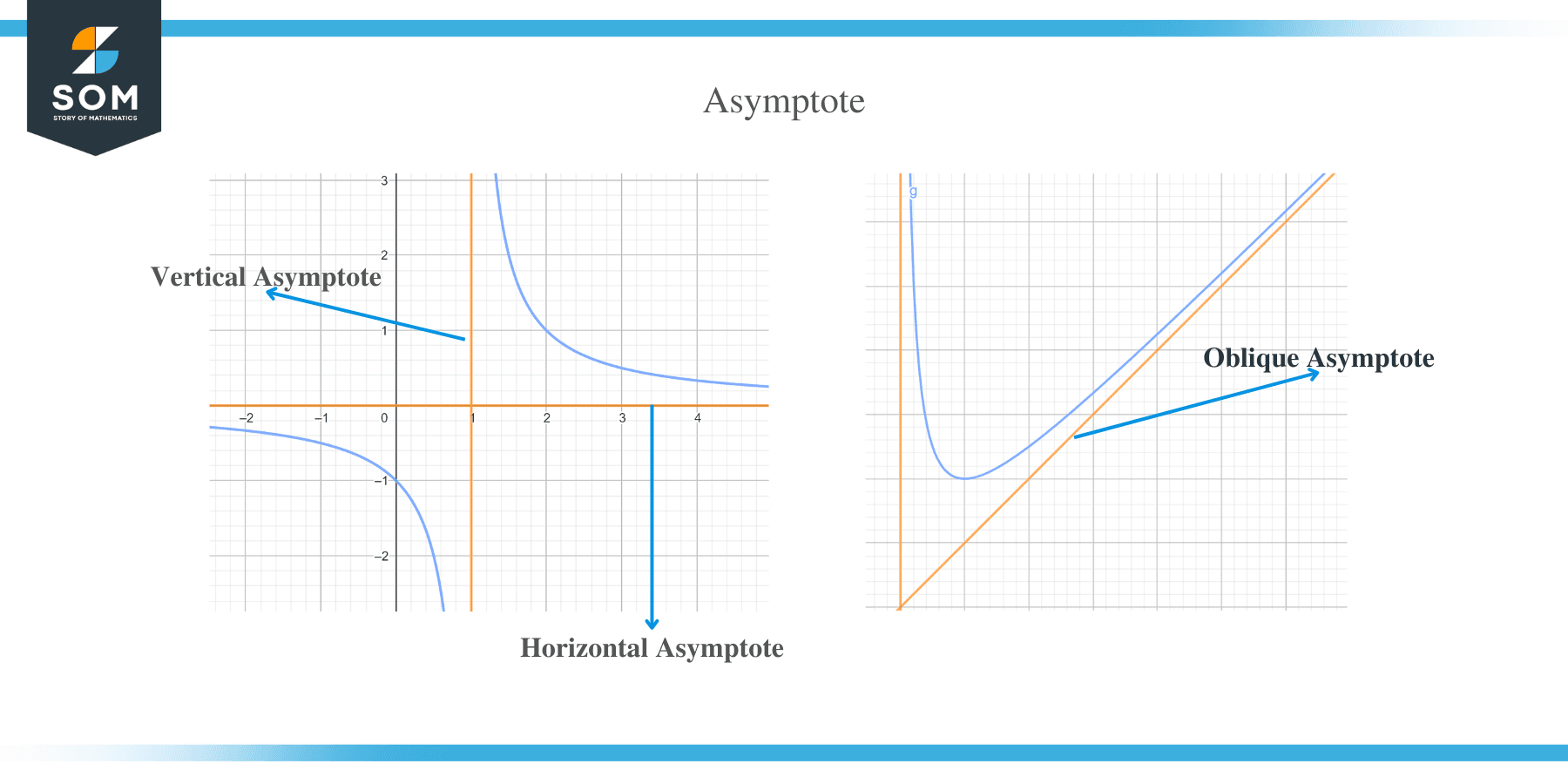
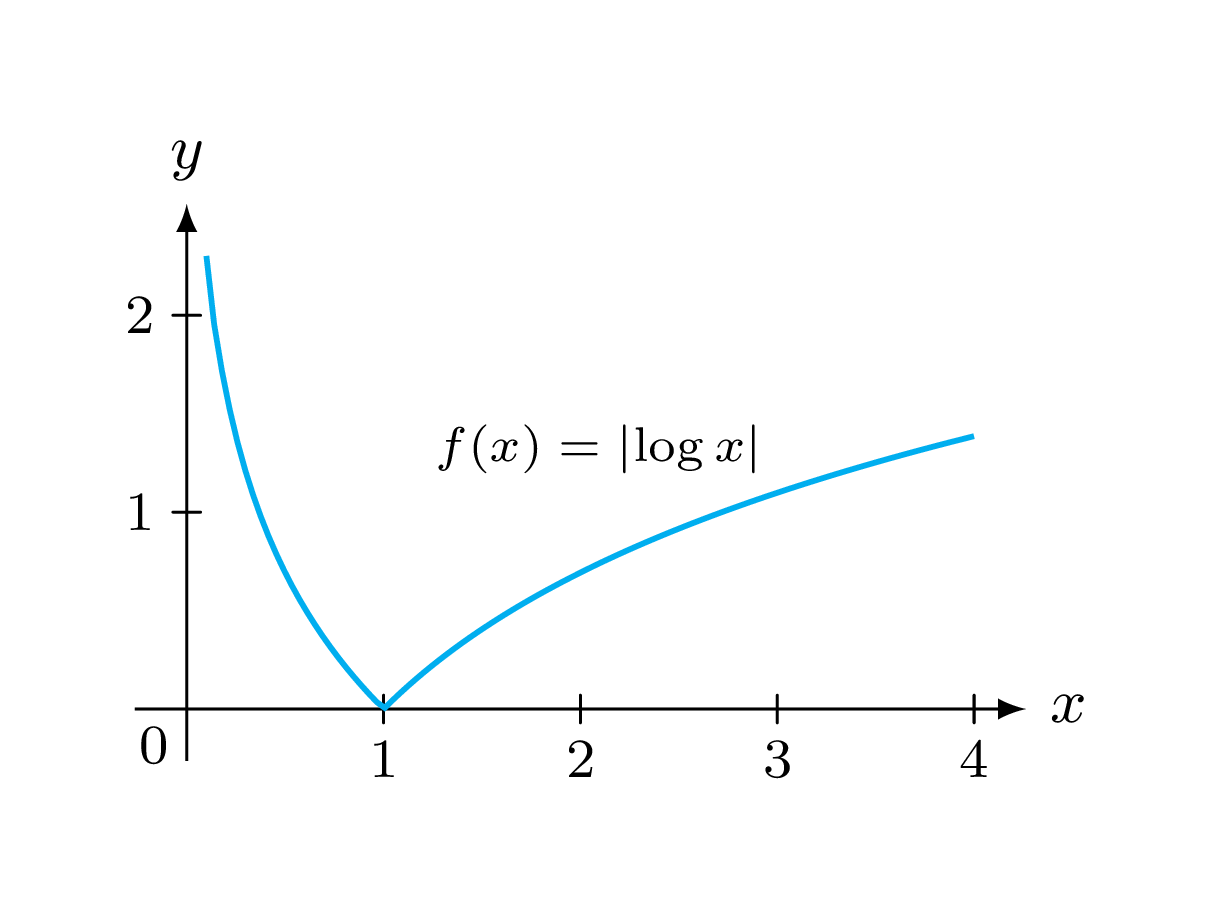
When you graph a logarithmic function, you’ll notice that it has a distinctive curve that never touches the x-axis. This is because the logarithm of 0 is undefined, so the graph will approach but never reach the x-axis.
The graph of a basic log function like y = log(x) will start at (-infinity, 0) and then curve upwards to the right. As x approaches infinity, y approaches infinity as well, creating an asymptotic relationship.
Logarithmic functions have a base that can affect the shape of the graph. For example, changing the base from 10 to 2 will compress the graph horizontally, making it steeper. The larger the base, the steeper the graph will appear.
Understanding the graph of a log function is essential for solving logarithmic equations and interpreting real-world data. By visualizing the relationship between logarithms and exponentials, you can gain a deeper appreciation for the power of these functions.
Next time you encounter a log function, take a moment to sketch out its graph. By understanding the key features and behaviors of logarithmic functions, you can enhance your mathematical intuition and problem-solving skills.
Graphs Of Logarithmic Function Explanation Examples
Tikz Pgf Help Me In Drawing Log x Curve TeX LaTeX Stack Exchange