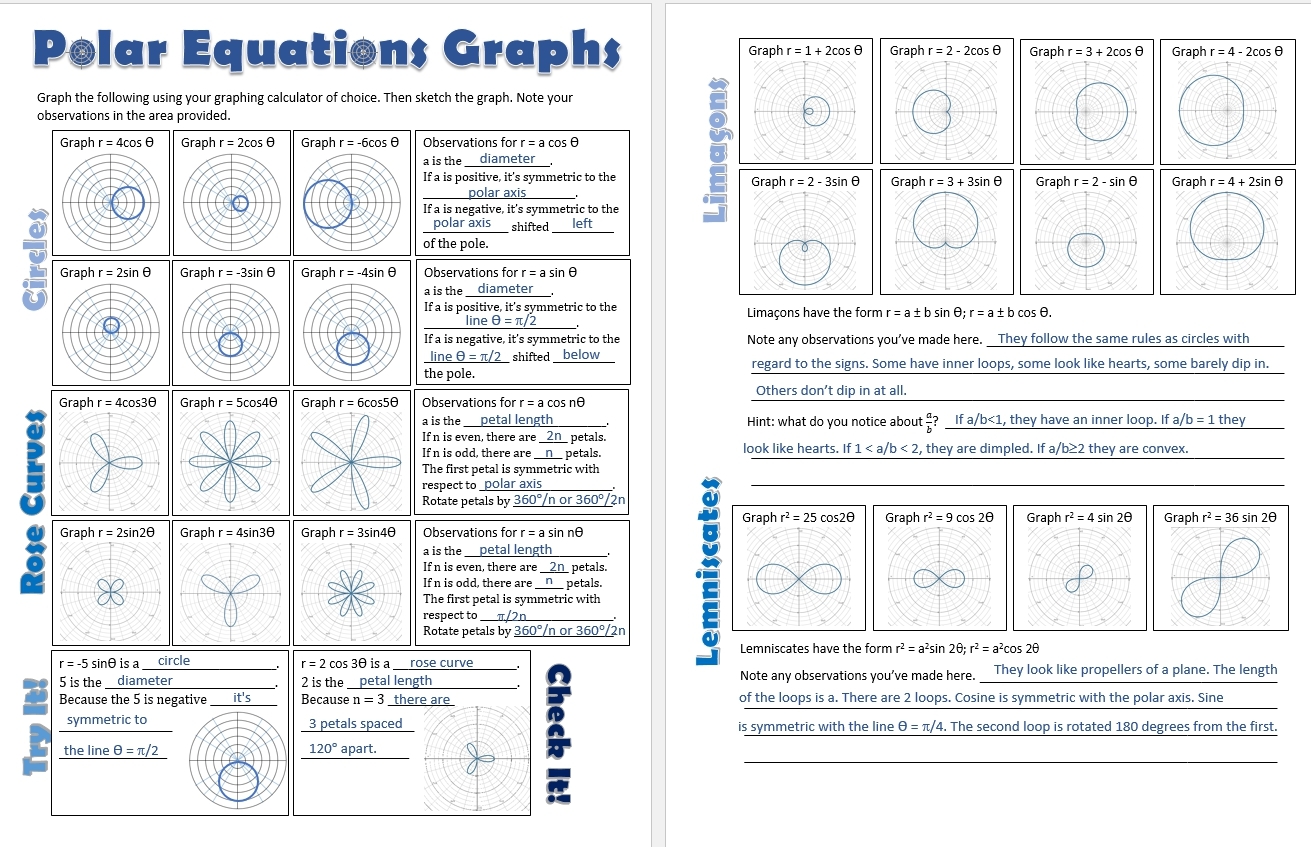
Are you curious about polar coordinates and how they can be represented graphically? You’re in the right place! Today, we’ll explore the fascinating world of graphs of different polar coordinates.
Polar coordinates provide a unique way to locate points in a plane using a distance and an angle. When these coordinates are graphed, they form beautiful and intricate patterns that are not seen in the Cartesian coordinate system.
Graphs Of Differnt Polar Coordinates
Graphs Of Different Polar Coordinates
One of the most basic polar graphs is the circle, which is represented by the equation r = a, where ‘a’ is the radius of the circle. As the angle changes, the distance from the origin remains constant, creating a perfect circle.
Another common polar graph is the cardioid, which resembles a heart shape. It is represented by the equation r = a + a*sin(theta), where ‘a’ determines the size of the cardioid. As the angle increases, the curve forms a distinct heart shape.
Moving on to more complex graphs, the spiral is created by equations like r = a + b*theta. This type of graph forms a spiral pattern that extends infinitely outward or inward, depending on the values of ‘a’ and ‘b’.
Exploring graphs of different polar coordinates can be a fun and rewarding exercise, allowing you to appreciate the beauty and versatility of this coordinate system. Whether you’re a math enthusiast or just curious about new concepts, polar graphs offer a unique perspective on geometry and visualization.
In conclusion, graphs of different polar coordinates offer a creative way to represent mathematical concepts visually. By exploring these graphs, you can gain a deeper understanding of how distance and angle work together to create intricate patterns on a plane. So grab a pencil and start sketching your own polar graphs today!
Polar Coordinates Systry
7 08 Graphs Of Polar Equations