Quadratic graphs are a fundamental part of algebra and can be graphed on various scales to visualize their shape and behavior. One interesting way to display a quadratic graph is on a log scale, which can provide unique insights into its characteristics.
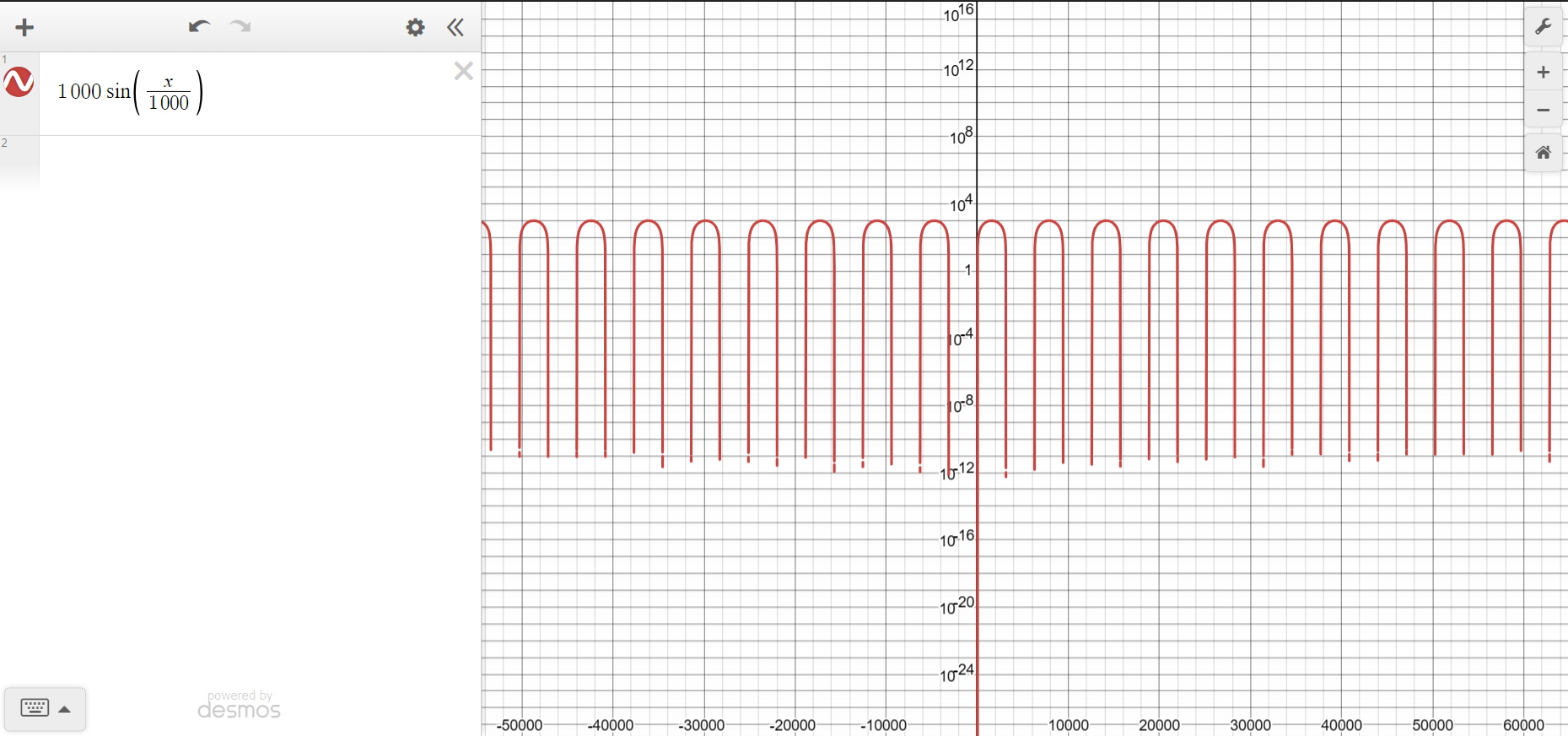
When graphing a quadratic function on a log scale, the x and y axes are represented differently compared to a regular linear scale. The x-axis typically represents the logarithm of the input values, while the y-axis remains the same, showing the output values.
Quadratic Graph On A Log Scale
Quadratic Graph On A Log Scale
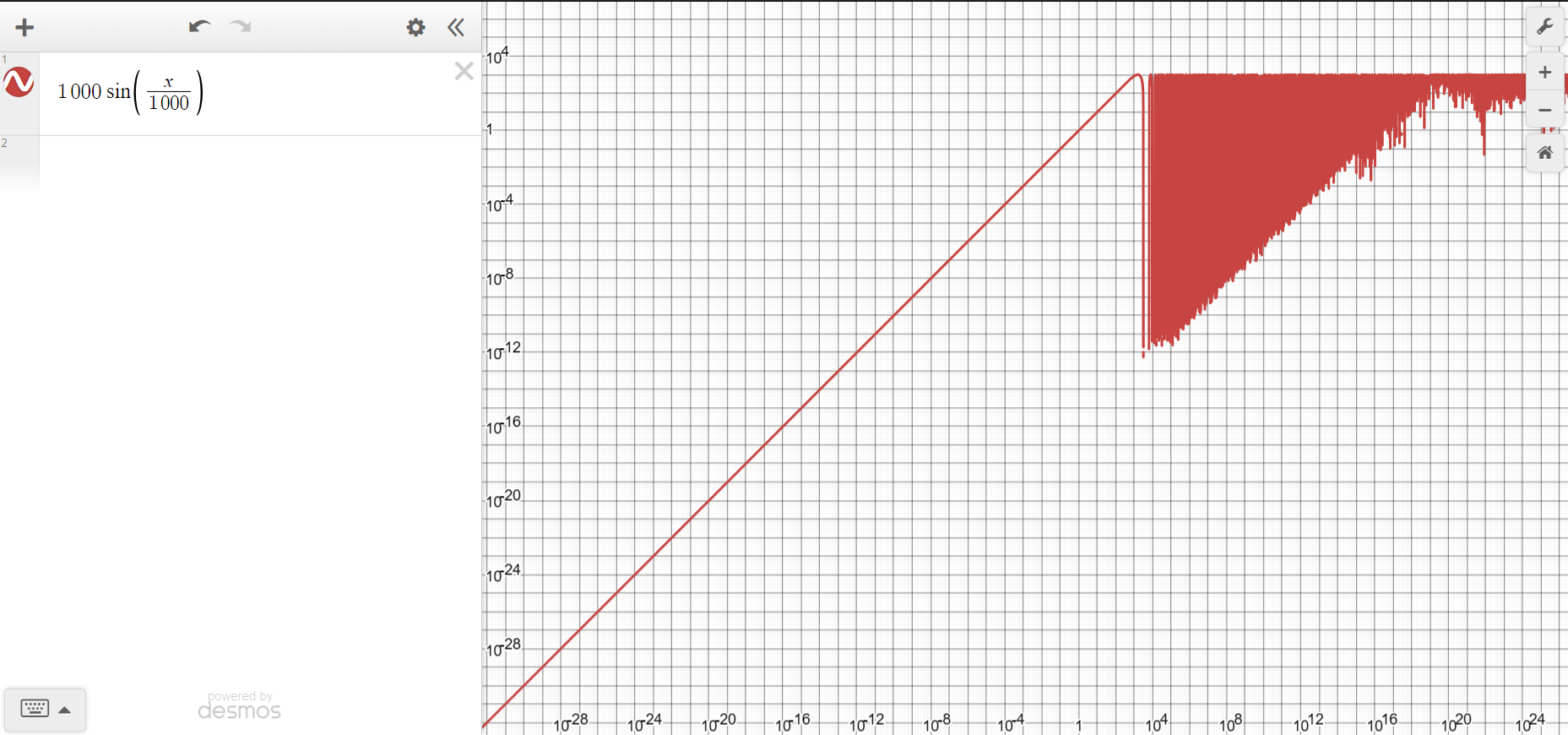
One advantage of graphing a quadratic function on a log scale is that it can help visualize exponential growth or decay more clearly. This can be especially useful in fields like economics, biology, and physics where exponential relationships are common.
On a log scale, the steepness of the quadratic curve can be better understood, as the logarithmic transformation compresses the x-axis values, emphasizing changes in certain regions of the graph. This can reveal patterns that may not be as apparent on a linear scale.
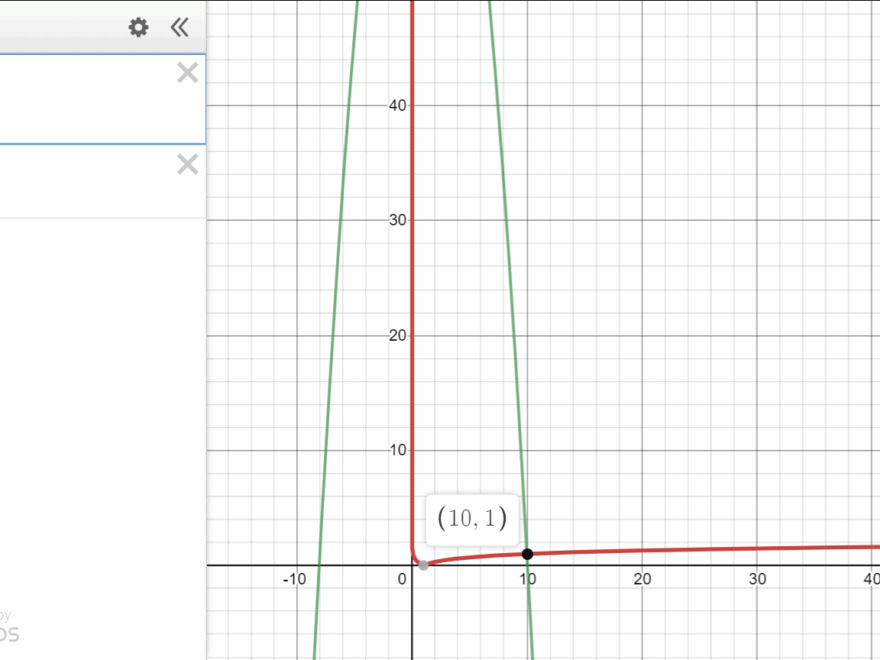
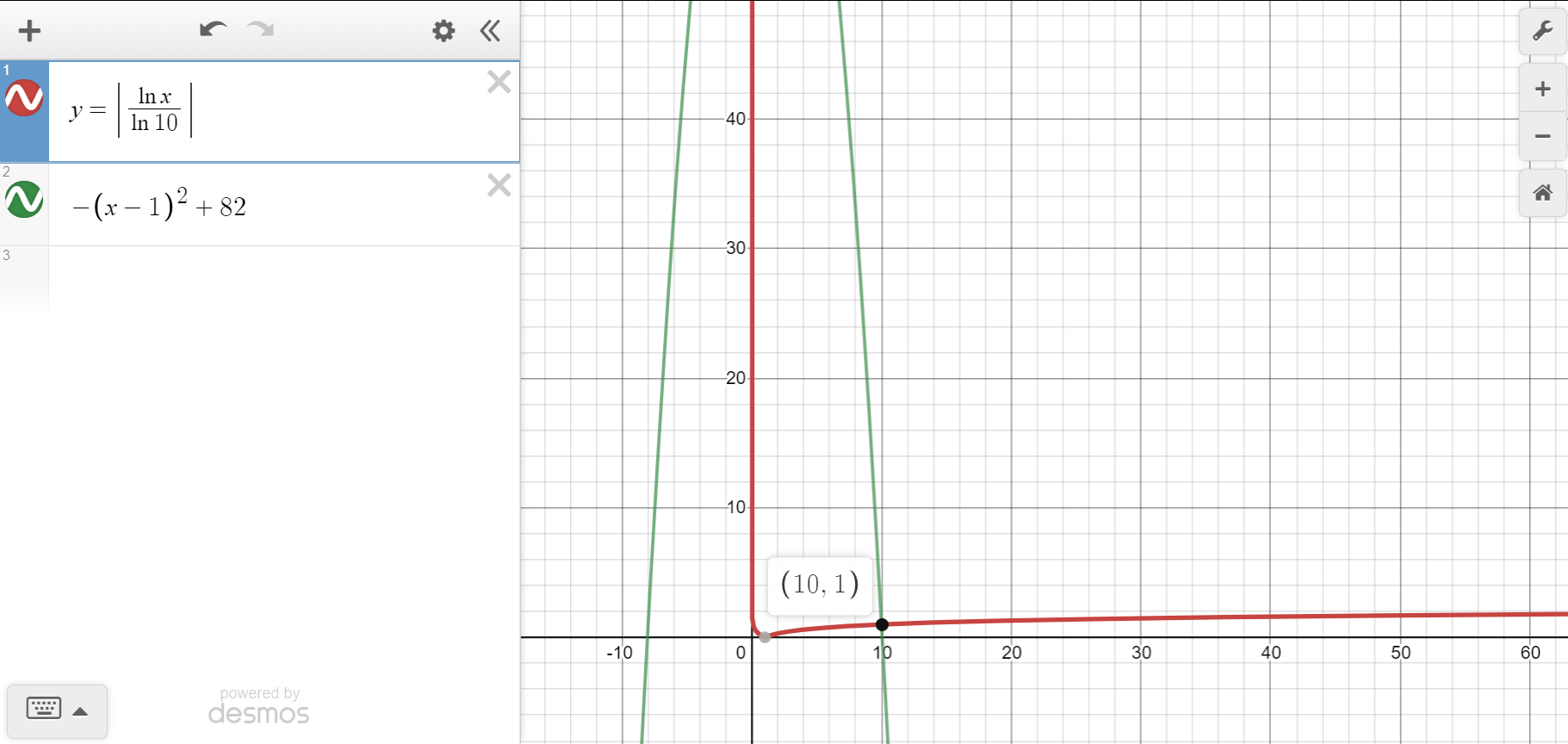
Additionally, graphing a quadratic function on a log scale can help identify asymptotes, zeros, and other key features more easily. By transforming the axes, the graph can be manipulated to highlight specific points of interest, providing a deeper understanding of the function’s behavior.
In conclusion, graphing a quadratic function on a log scale offers a unique perspective that can enhance our interpretation of the data. By visualizing the function in this way, we can gain insights that may not be as readily apparent on a traditional linear scale, making it a valuable tool for analysis.
Graphing Functions Understanding Logarithmic Scale In A Graph Mathematics Stack Exchange
Logarithms Find The Intersection Point Of A Logarithmic And A Quadratic Functions Mathematics Stack Exchange