Are you struggling to understand the R Sin Theta graph and how it relates to trigonometry? Don’t worry, you’re not alone! Many students find this concept confusing at first, but with a little explanation, it can become much clearer.
When graphing R Sin Theta, you are essentially plotting points on a polar coordinate system. R represents the distance from the origin (0,0), while Theta represents the angle in standard position measured counterclockwise from the positive x-axis.
R Sin Theta Graph
The Basics of the R Sin Theta Graph
As you increase Theta from 0 to 2π, the graph of R Sin Theta will create a complete circle. This is because Sin Theta oscillates between -1 and 1 as Theta varies, resulting in a periodic function that repeats every 2π.
Understanding the relationship between R and Theta is crucial in interpreting the graph accurately. For example, if R is constant and Theta changes, you will see a spiral pattern emerge. This demonstrates how R Sin Theta behaves as both variables fluctuate.
One common application of the R Sin Theta graph is in physics, particularly when describing waveforms or circular motion. By visualizing how R and Theta interact, scientists and engineers can better analyze and predict the behavior of complex systems.
In conclusion, mastering the R Sin Theta graph may seem daunting at first, but with practice and patience, you can confidently navigate its intricacies. Remember, this graph is a powerful tool for visualizing polar functions and understanding the relationship between distance and angle.
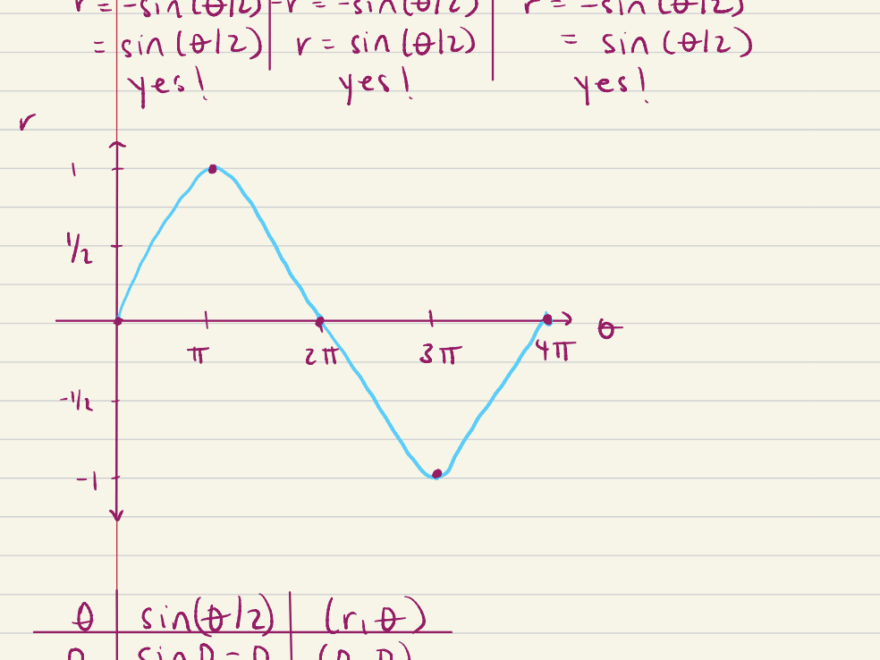
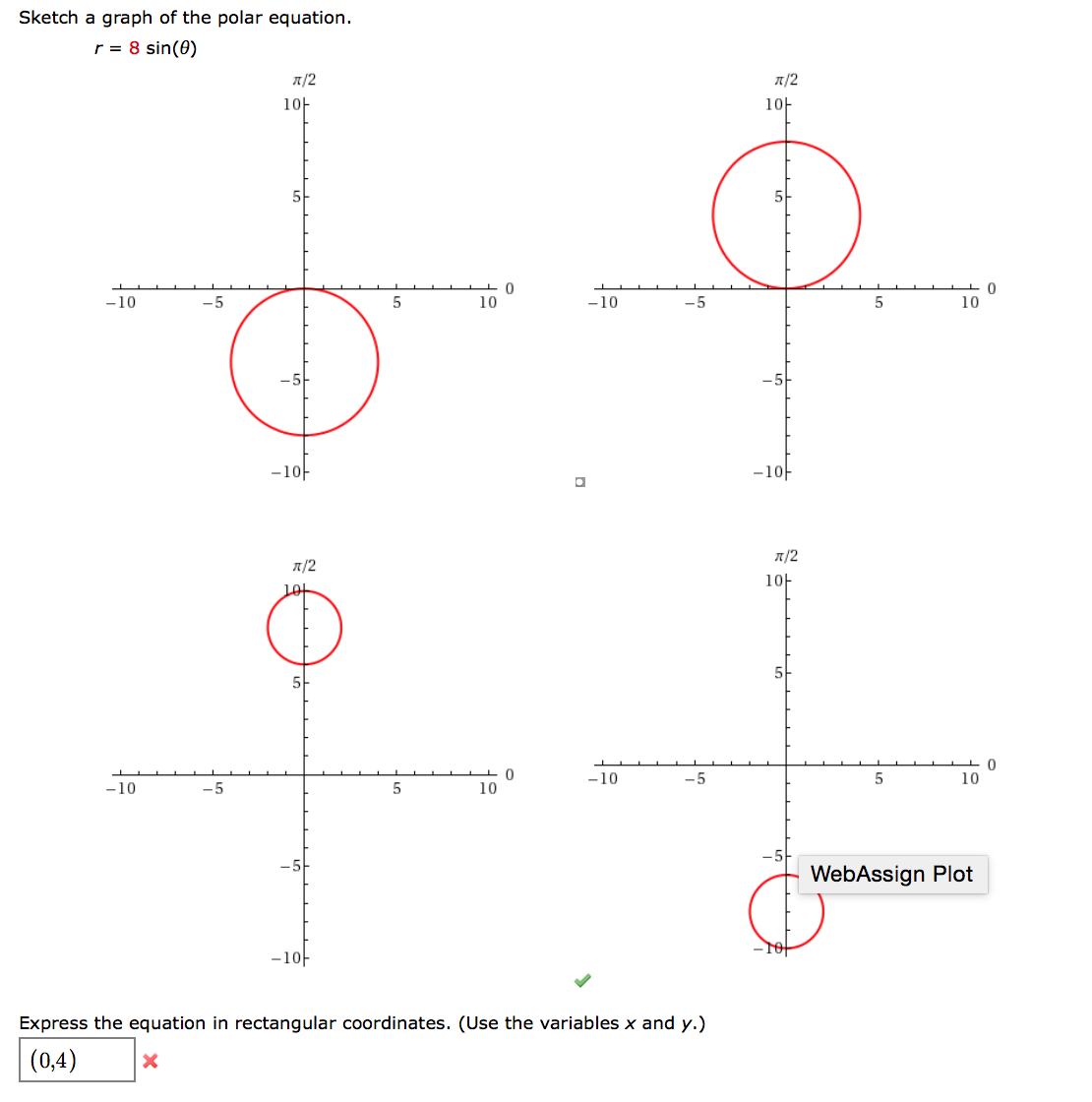
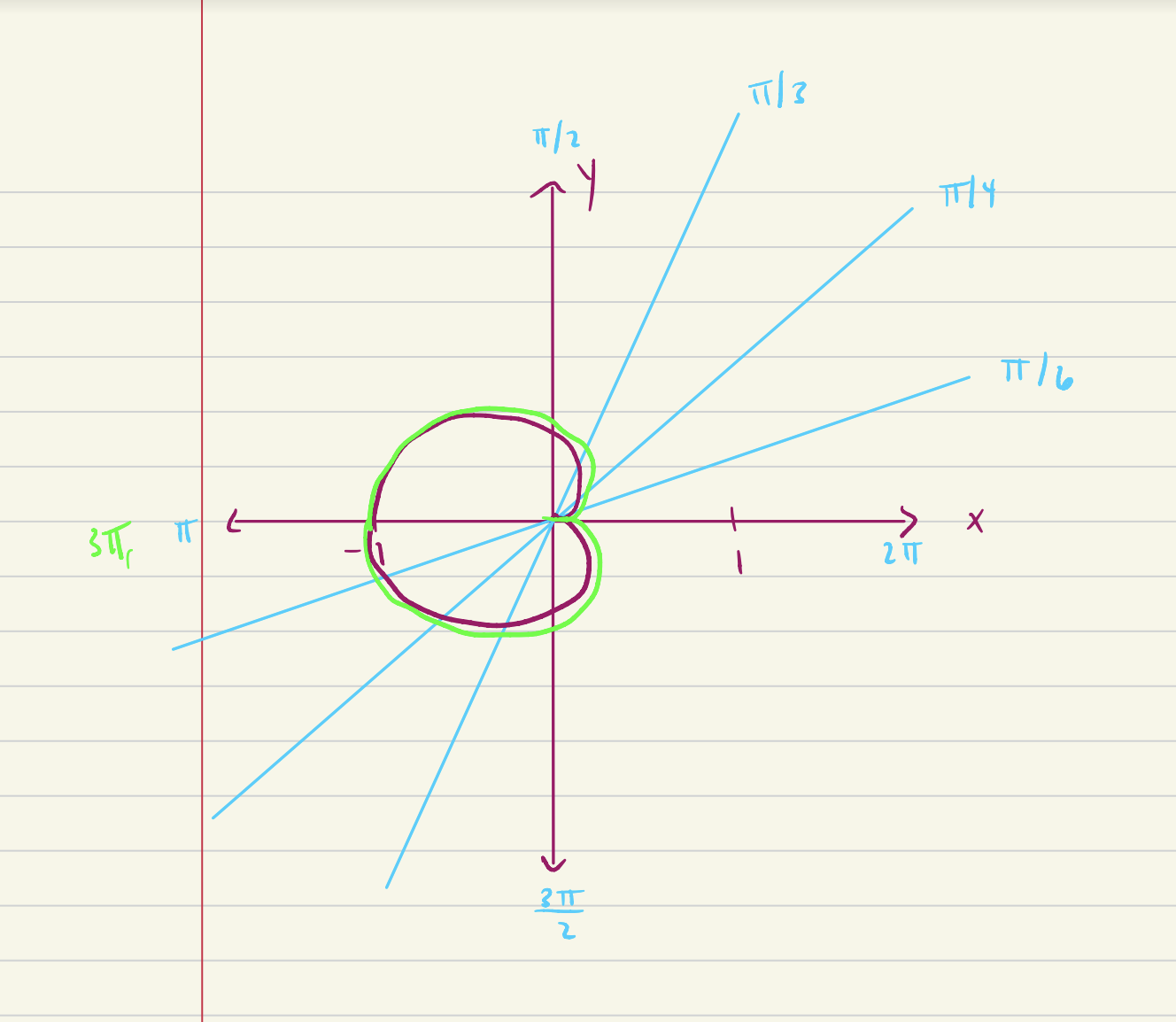
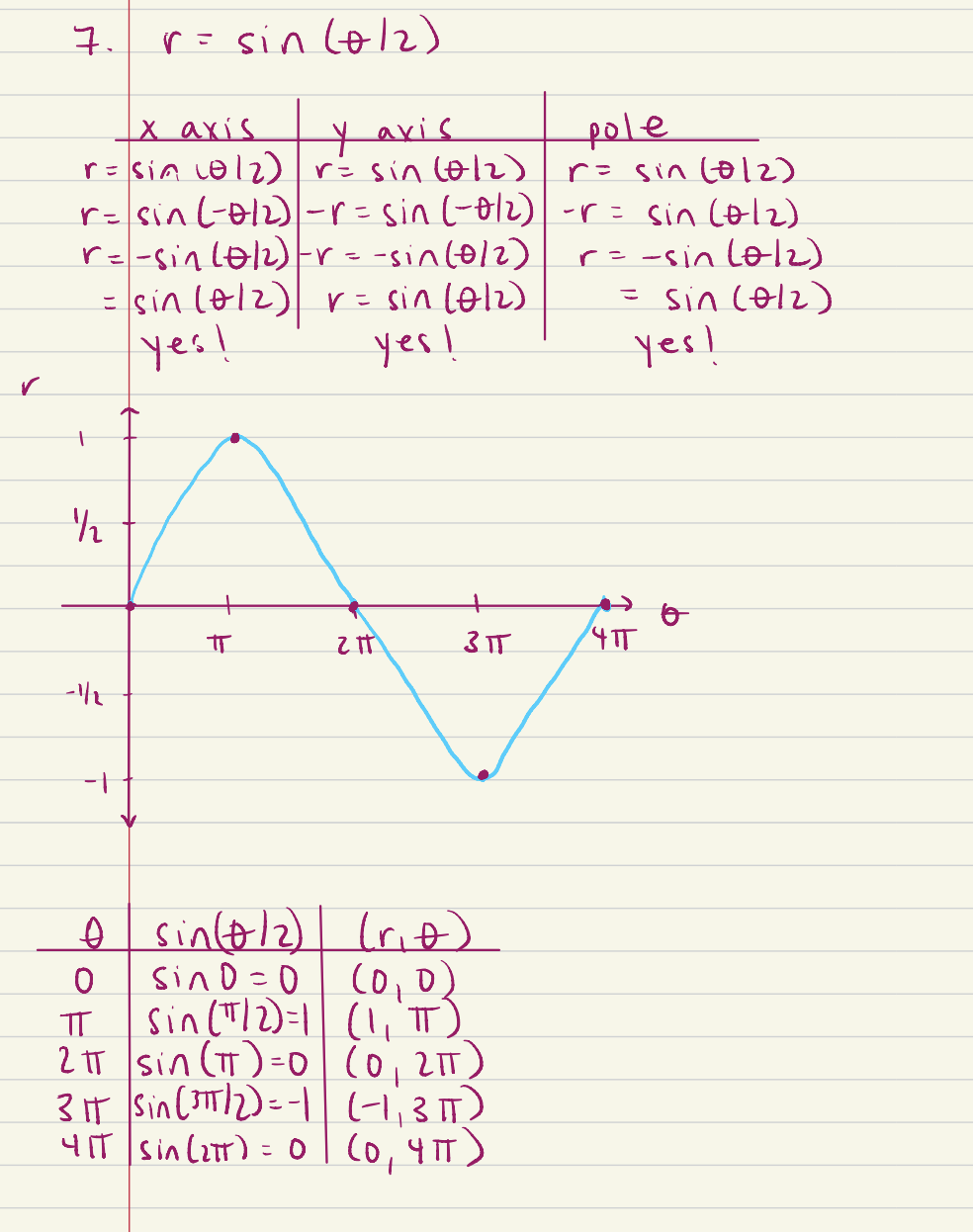
Need Help Graphing Polar Equation r sin frac theta 2 Mathematics Stack Exchange
Need Help Graphing Polar Equation r sin frac theta 2 Mathematics Stack Exchange