Are you struggling with understanding how to sketch graphs for different functions? Don’t worry, we’ve got you covered! Graphing functions can seem daunting at first, but with a little practice, you’ll be a pro in no time.
Whether you’re dealing with linear, quadratic, cubic, or exponential functions, each type has its own unique characteristics that can help you visualize the shape of the graph. By following a few simple steps, you’ll be able to sketch accurate graphs for any function.
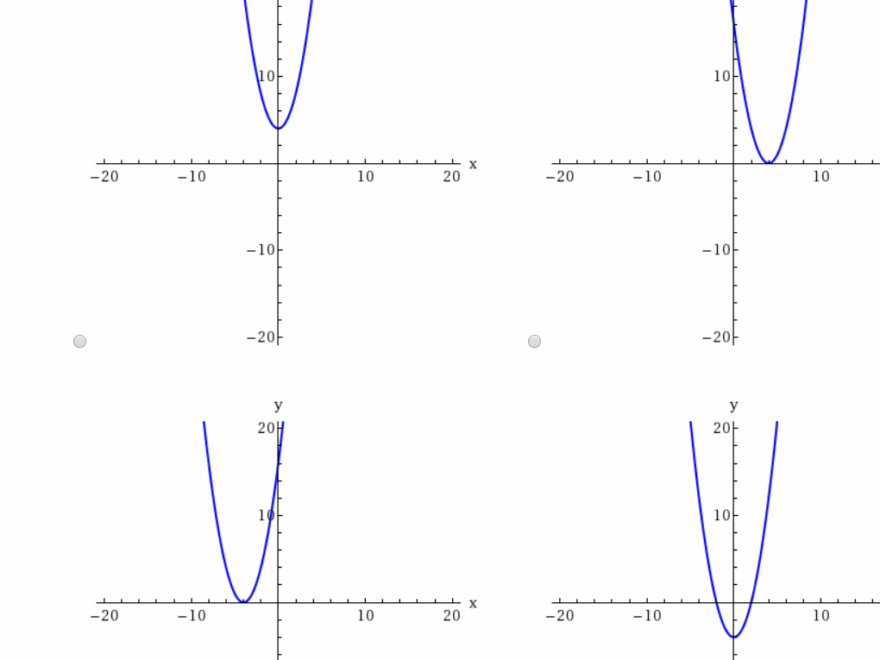
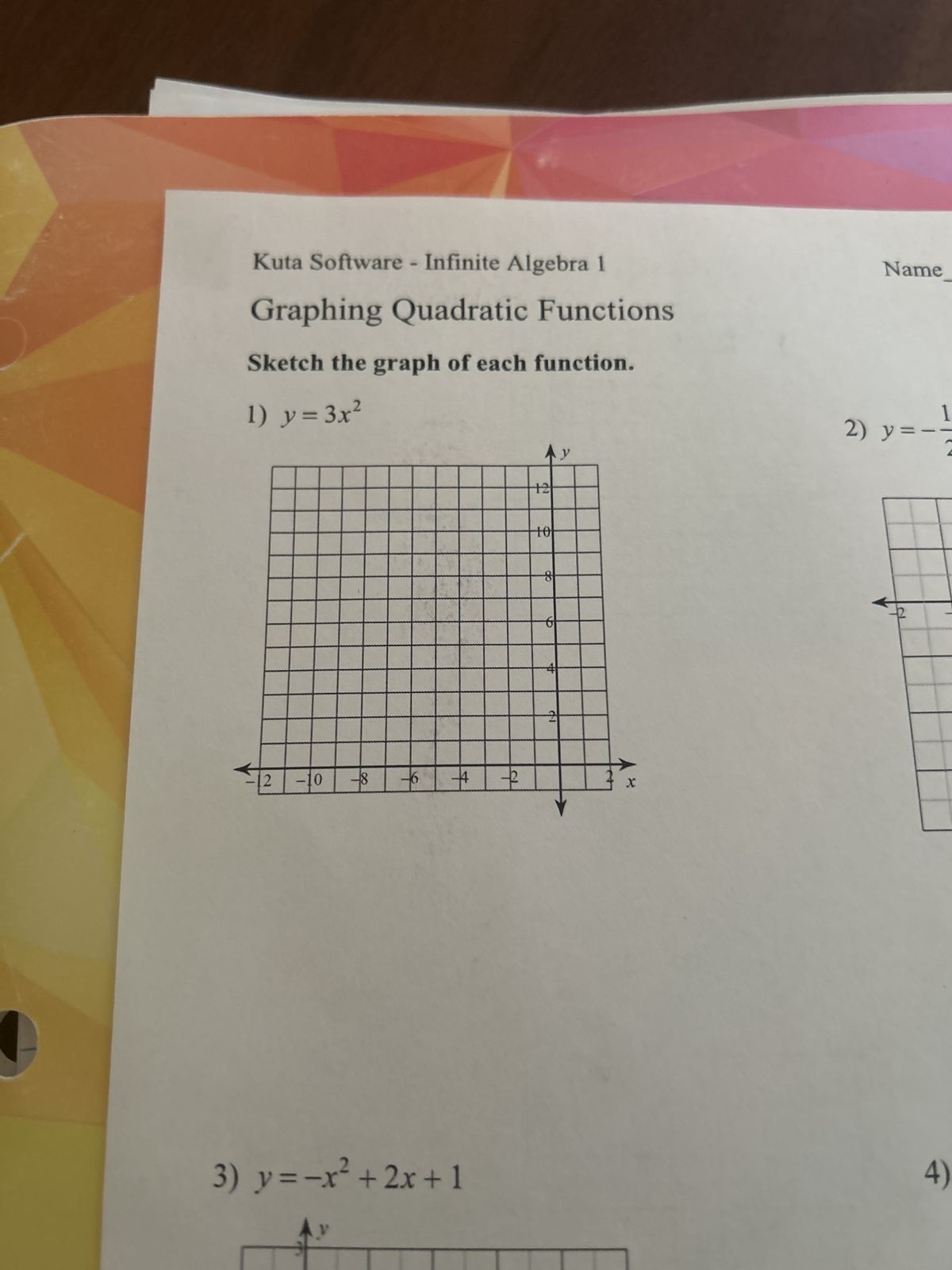
Sketch Graph For Each Function
Sketch Graph For Each Function
For linear functions, start by identifying the slope and y-intercept. The slope determines how steep the line is, while the y-intercept tells you where the line crosses the y-axis. Plot these points and connect them to create a straight line.
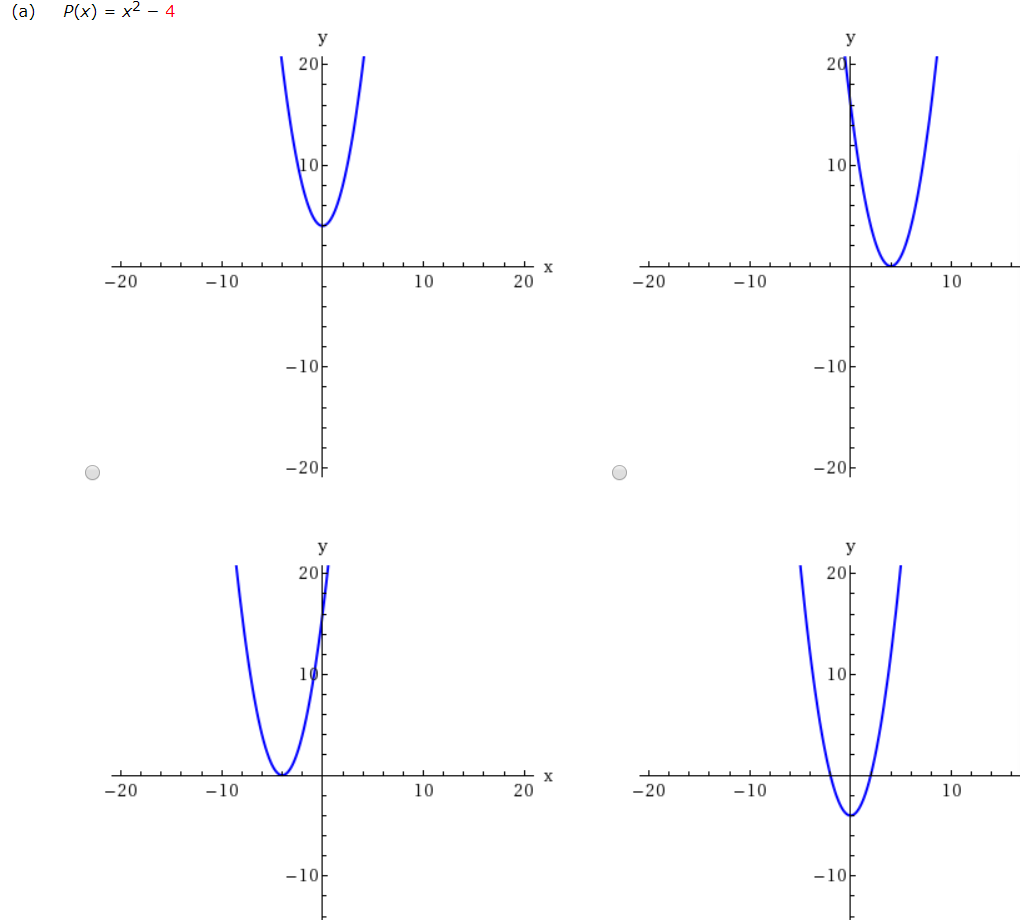
Quadratic functions have a parabolic shape. Find the vertex, which is the highest or lowest point on the graph, and the x-intercepts, where the graph crosses the x-axis. Use these points to sketch a smooth curve that opens upwards or downwards.
Cubic functions have a more complex shape with two bends. Locate the x-intercepts, where the graph crosses the x-axis, and any other key points such as local maxima or minima. Connect these points to create a curve that changes direction twice.
Exponential functions grow or decay exponentially. Identify the base of the function, which determines the rate of growth or decay, and the y-intercept. Plot these points and sketch a curve that either increases or decreases rapidly depending on the base.
With a little practice and understanding of the characteristics of each function, sketching graphs will become second nature. Remember to pay attention to key points such as intercepts, vertices, and points of inflection to create accurate and visually appealing graphs.
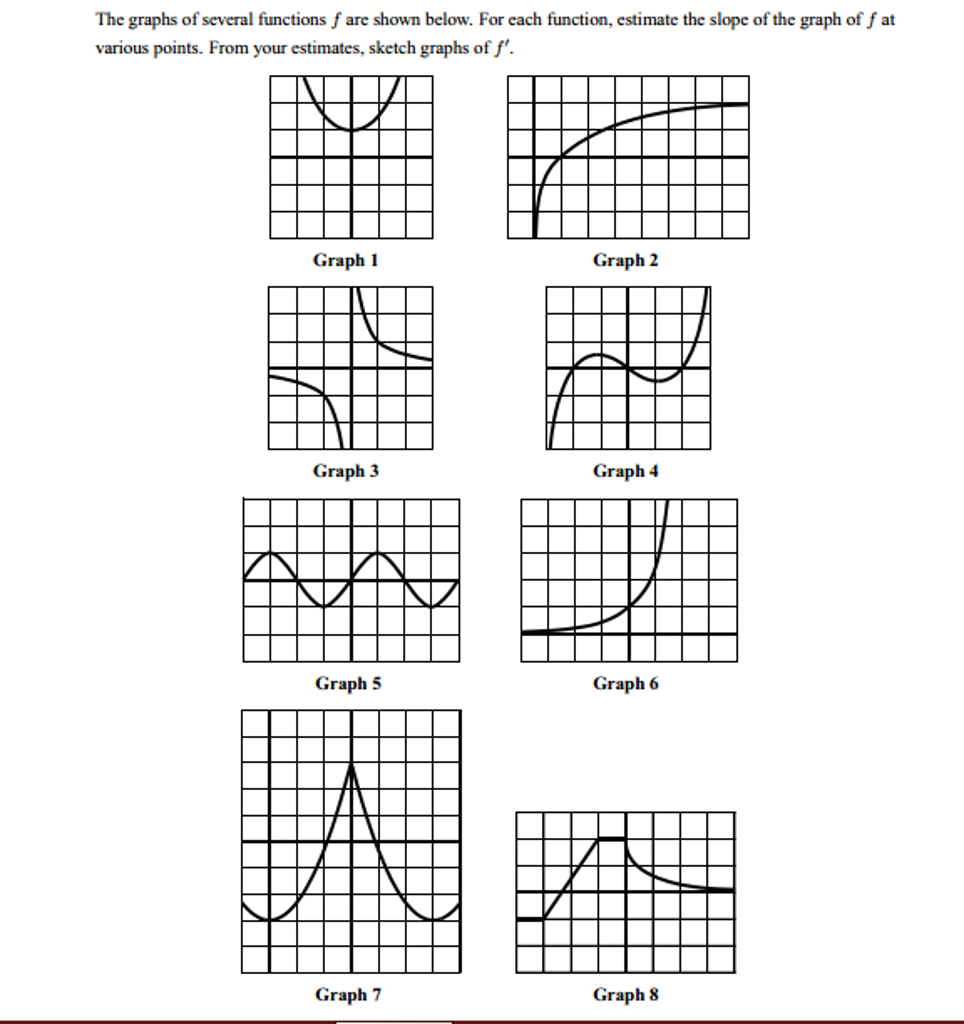
Solved The Graphs Of Several Functions F Are Shown Below Chegg
Solved Sketch The Graph Of Each Function By Transforming The Chegg