Have you ever struggled with calculus problems involving numerical integration? Fear not! The trapezoidal rule is here to save the day. This handy method helps approximate the area under a curve, making calculus a bit more manageable.
Whether you’re a student studying for a math exam or a professional dealing with real-world applications, understanding the trapezoidal rule can be a game-changer. It’s a simple yet powerful tool that can make your life a whole lot easier when dealing with integrals.
Trapezoidal Rule Calc 2 Graph
Trapezoidal Rule Calc 2 Graph
Imagine you have a graph with a curve that you need to find the area under. Calculating this by hand can be tedious and prone to errors. That’s where the trapezoidal rule comes in. It breaks down the area into trapezoids, making the calculation more straightforward.
By dividing the area under the curve into trapezoids, the trapezoidal rule provides a close approximation of the integral. This method is especially useful when dealing with functions that are difficult to integrate analytically. It’s like having a cheat code for calculus!
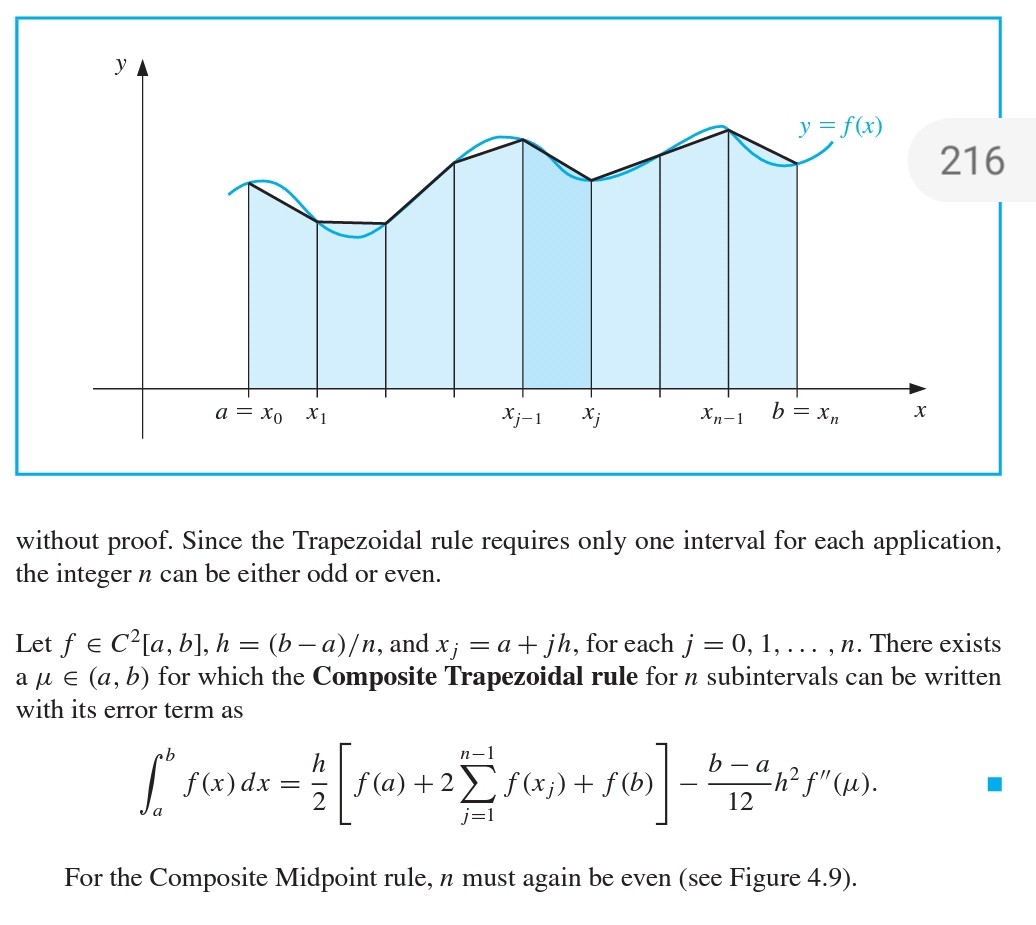
So, how does the trapezoidal rule work in practice? First, you divide the interval of integration into smaller segments. Then, you approximate the curve within each segment using straight lines. Finally, you calculate the area of each trapezoid and sum them up to get an estimate of the total area under the curve.
In conclusion, the trapezoidal rule is a valuable tool for approximating integrals, especially when dealing with complex functions or large datasets. By breaking down the area under a curve into simpler shapes, this method simplifies the integration process and provides accurate results. Give it a try next time you’re faced with a challenging calculus problem!
Algebra Precalculus Need Help To Understand Different Formula For Trapezoidal s Rule Mathematics Stack Exchange
11 03 Approximate Areas Under Graphs Using Trapezoidal Rule Standard Level Maths IB Applications And Interpretation SL 2021 Edition Mathspace